题目
证明:(Acup B)-B=A-AB=AB=A-B.
证明: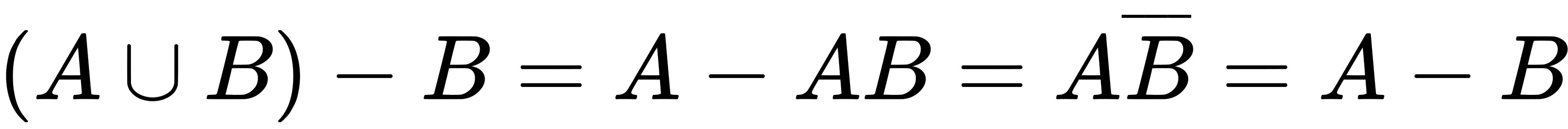 .
.
题目解答
答案
【答案】
见解析
【解析】
由定义得: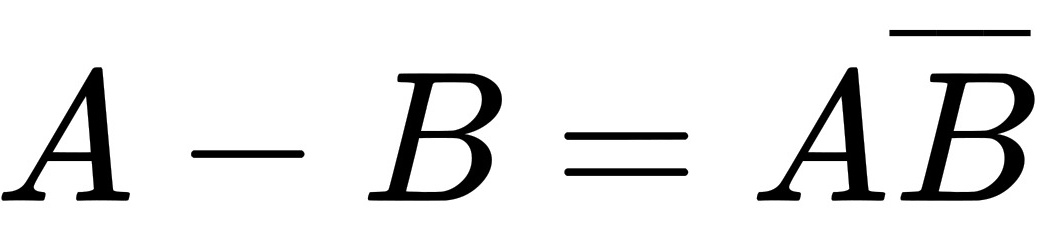 ,并且
,并且
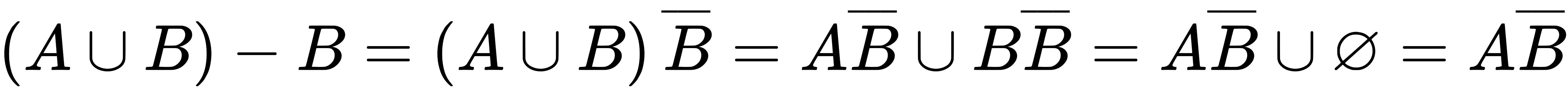 ,
,
而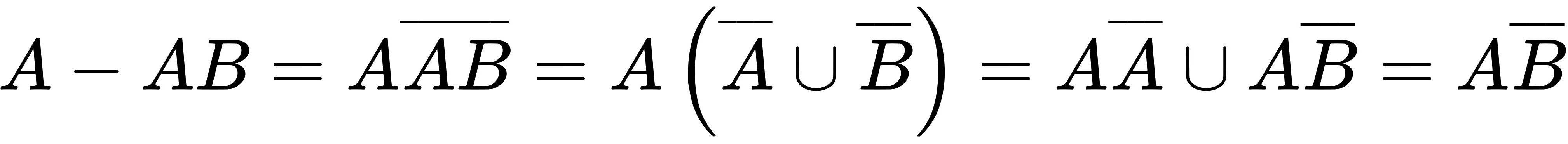 .
.
所以等式成立.
解析
考查要点:本题主要考查集合运算的基本性质,特别是集合的并集、交集、补集以及差集之间的关系。需要熟练掌握集合运算的定义及等价变形。
解题核心思路:通过集合运算的定义,逐步推导各表达式之间的等价性。关键点在于:
- 差集的定义:$A - B = \{x \mid x \in A \text{ 且 } x \notin B\}$;
- 并集与差集的关系:$(A \cup B) - B = A - B$;
- 交集与差集的关系:$A - (A \cap B) = A - B$;
- 补集与交集的转换:$A \cap \overline{B} = A - B$。
证明步骤
1. 证明 $(A \cup B) - B = A - B$
- 根据差集的定义:
$(A \cup B) - B = \{x \mid x \in A \cup B \text{ 且 } x \notin B\}$ - 分析元素归属:
若 $x \in A \cup B$ 且 $x \notin B$,则 $x$ 必须属于 $A$(否则既不属于 $A$ 也不属于 $B$,与 $x \in A \cup B$ 矛盾)。因此:
$(A \cup B) - B = \{x \mid x \in A \text{ 且 } x \notin B\} = A - B$
2. 证明 $A - AB = A - B$
- 此处 $AB$ 表示 $A \cap B$:
$A - (A \cap B) = \{x \mid x \in A \text{ 且 } x \notin A \cap B\}$ - 简化条件:
$x \notin A \cap B$ 等价于 $x \notin B$(因为 $x \in A$ 已经满足)。因此:
$A - (A \cap B) = \{x \mid x \in A \text{ 且 } x \notin B\} = A - B$
3. 证明 $A\overline{B} = A - B$
- 此处 $A\overline{B}$ 表示 $A \cap \overline{B}$:
$A \cap \overline{B} = \{x \mid x \in A \text{ 且 } x \in \overline{B}\}$ - 补集的定义:
$x \in \overline{B}$ 等价于 $x \notin B$,因此:
$A \cap \overline{B} = \{x \mid x \in A \text{ 且 } x \notin B\} = A - B$
4. 结论
通过上述推导可知:
$(A \cup B) - B = A - (A \cap B) = A \cap \overline{B} = A - B$