题目
曲线 ) (x)^2-(y)^2+(z)^2=0 z=1 .
曲线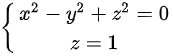 在
在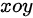 坐标面上的投影曲线方程为______
坐标面上的投影曲线方程为______
A.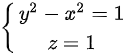
B.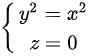
C.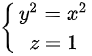
D.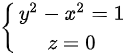
题目解答
答案
根据曲线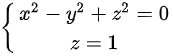 将
将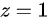 代入
代入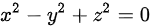 得到
得到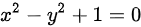 ,
,
化简后可求得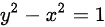
由于求曲线在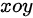 面上的投影,则需满足
面上的投影,则需满足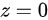 ,
,
二者联立可得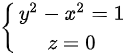 故选择D项
故选择D项
解析
步骤 1:代入$z=1$
将$z=1$代入方程${x}^{2}-{y}^{2}+{z}^{2}=0$,得到${x}^{2}-{y}^{2}+1=0$。
步骤 2:化简方程
化简方程${x}^{2}-{y}^{2}+1=0$,得到${y}^{2}-{x}^{2}=1$。
步骤 3:确定投影条件
由于求曲线在xoy面上的投影,因此需要满足$z=0$。
步骤 4:联立方程
将步骤2和步骤3的方程联立,得到$\left \{ \begin{matrix} {y}^{2}-{x}^{2}=1\\ z=0\end{matrix} \right.$。
将$z=1$代入方程${x}^{2}-{y}^{2}+{z}^{2}=0$,得到${x}^{2}-{y}^{2}+1=0$。
步骤 2:化简方程
化简方程${x}^{2}-{y}^{2}+1=0$,得到${y}^{2}-{x}^{2}=1$。
步骤 3:确定投影条件
由于求曲线在xoy面上的投影,因此需要满足$z=0$。
步骤 4:联立方程
将步骤2和步骤3的方程联立,得到$\left \{ \begin{matrix} {y}^{2}-{x}^{2}=1\\ z=0\end{matrix} \right.$。