求微分方程ln xdy+(y-ln x)dx=0满足条件ln xdy+(y-ln x)dx=0的特解..
求微分方程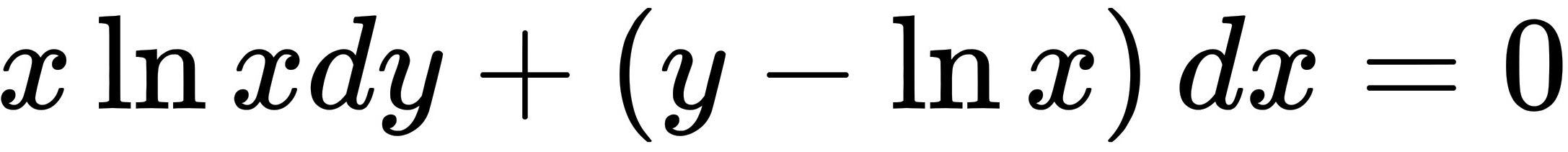 满足条件
满足条件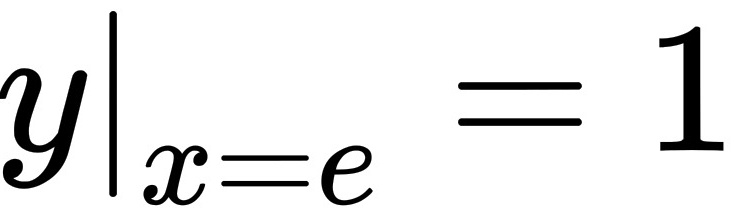 的特解.
的特解.
题目解答
答案
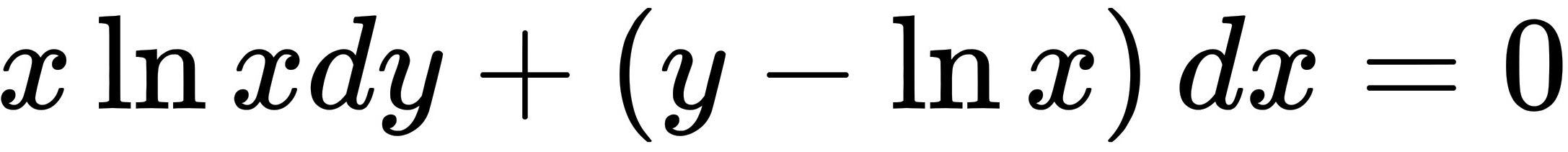 ,
,
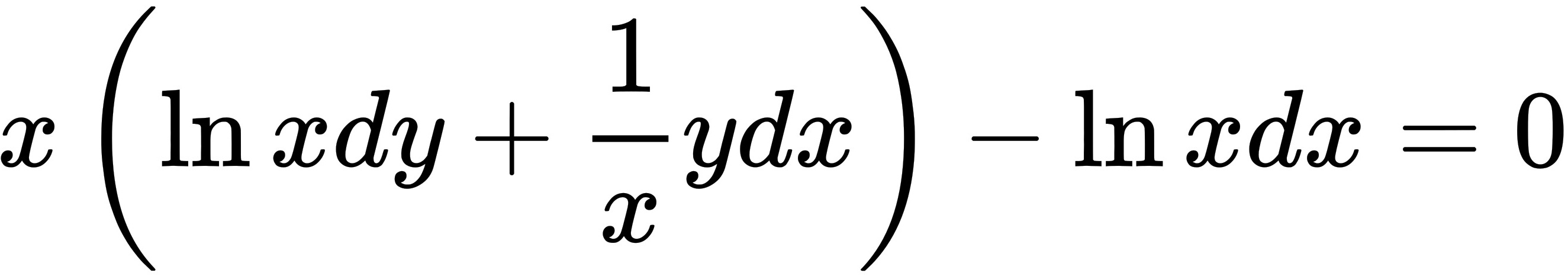 ,
,
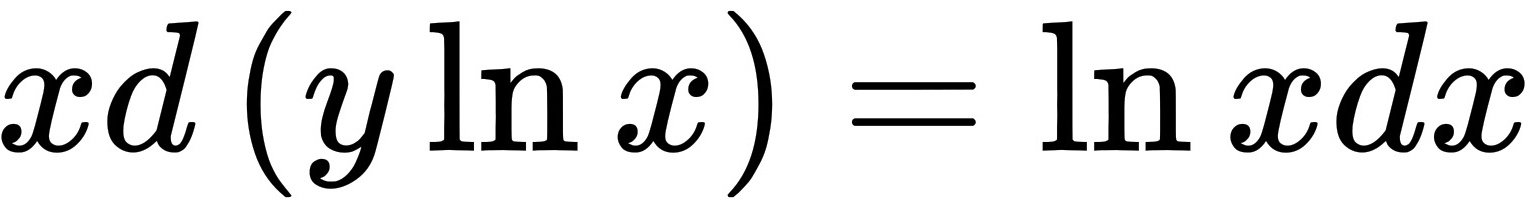 ,
,
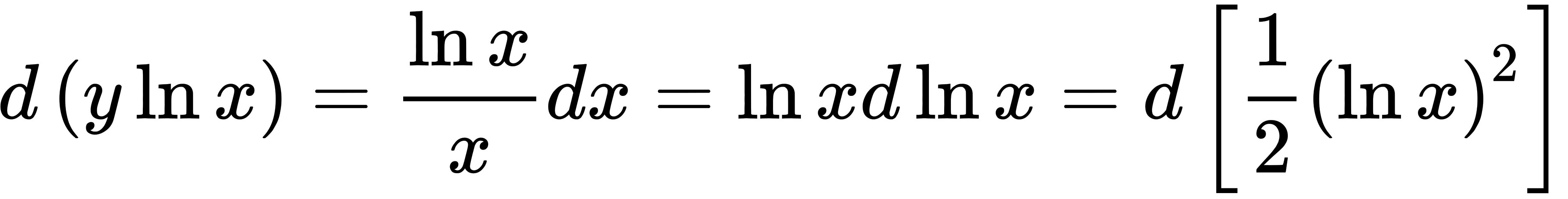 ;
;
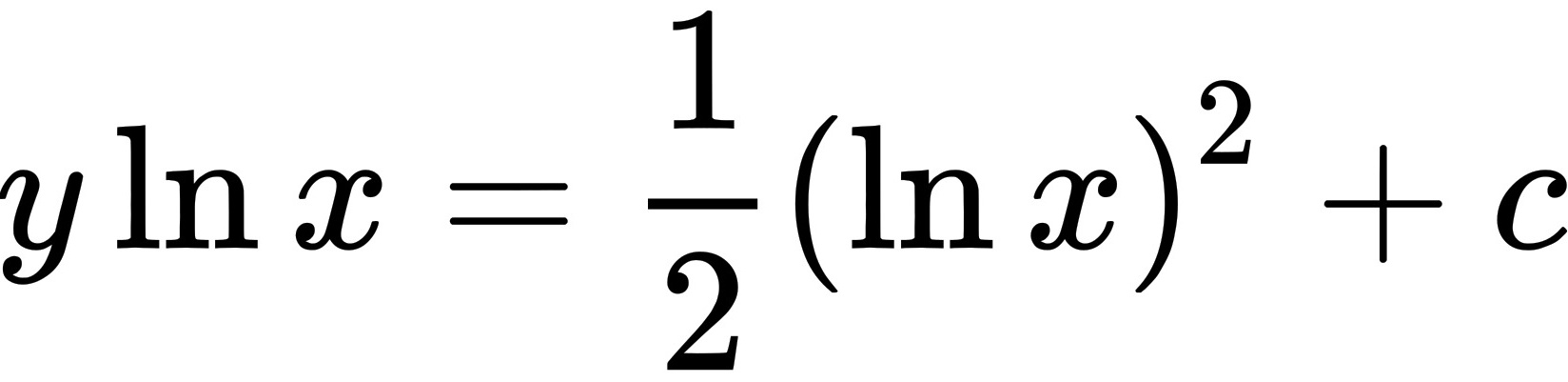 ,c为任意常数,
,c为任意常数,
由于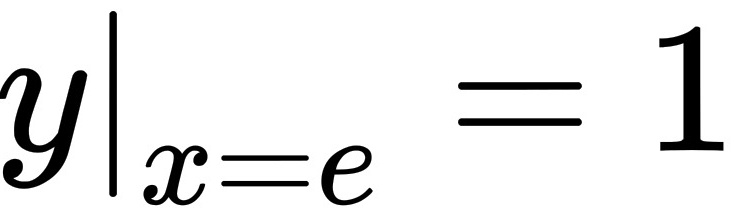 ,
,
所以,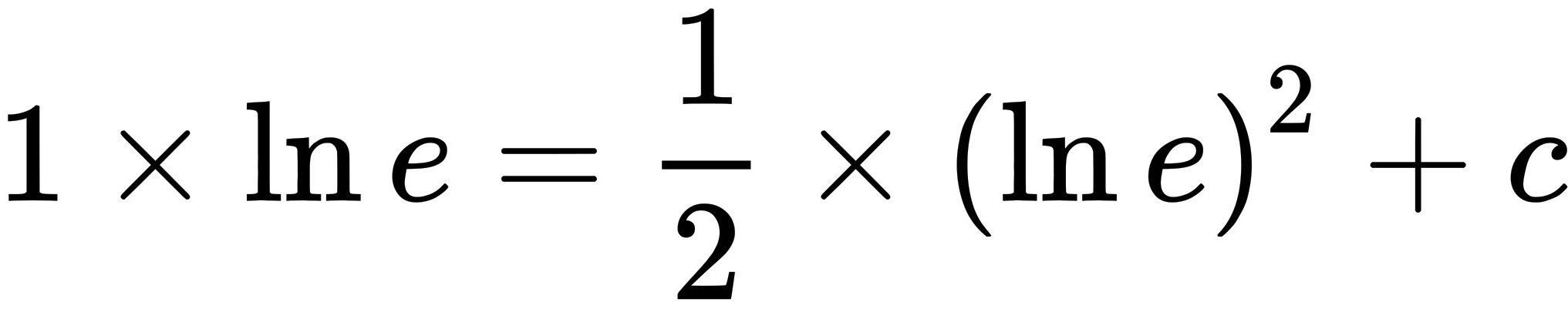
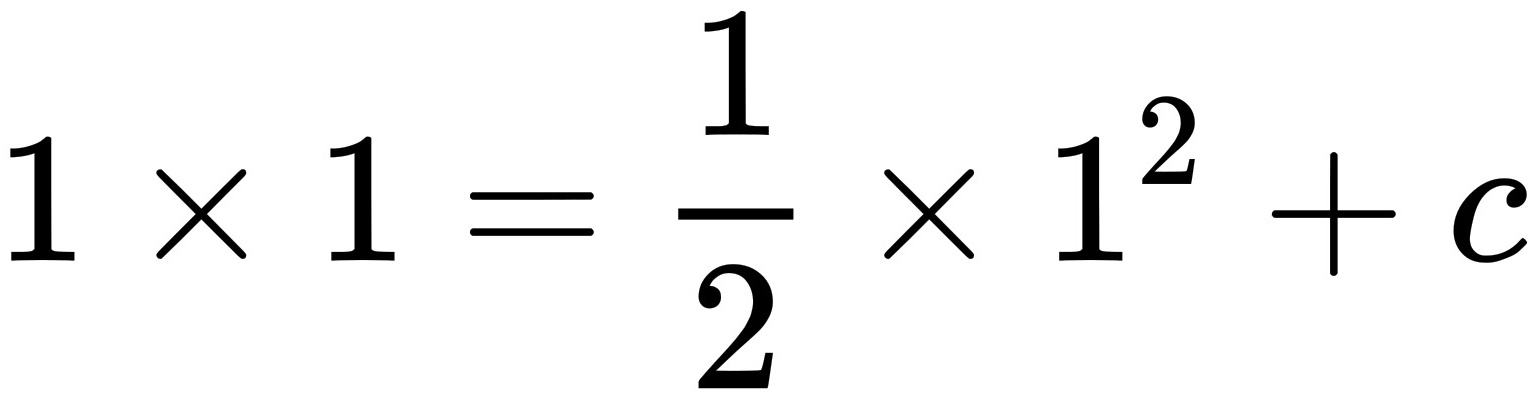
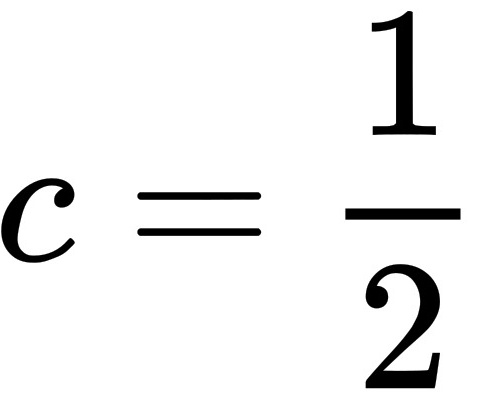
所以,微分方程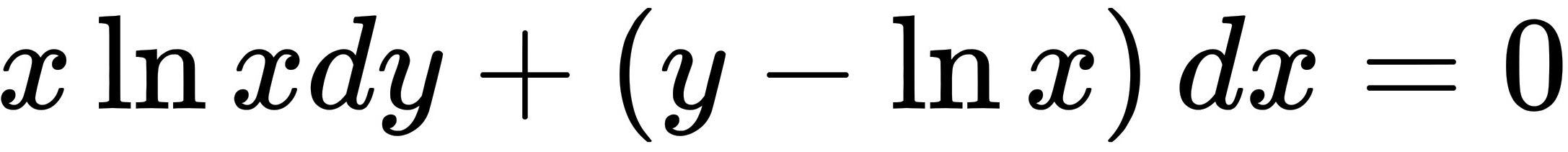 满足条件
满足条件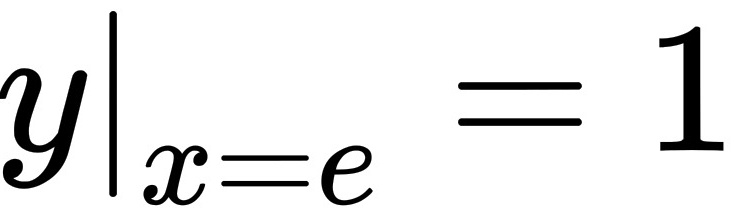 的特解为
的特解为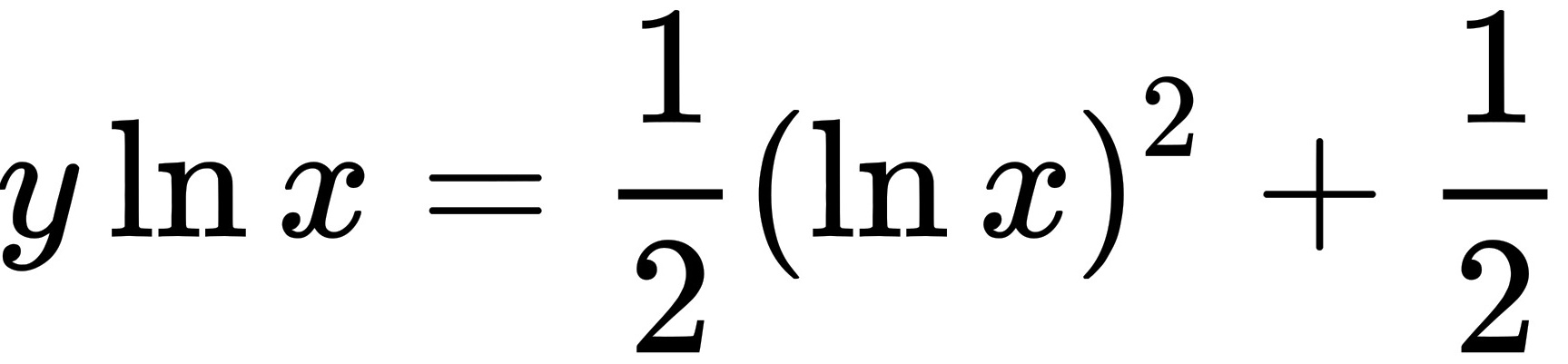 .
.
解析
考查要点:本题主要考查微分方程的求解,特别是通过恰当方程或变量替换的方法将方程转化为可积分形式。
解题核心思路:
- 观察方程结构,尝试将方程整理为全微分形式。
- 引入变量替换(如 $v = y \ln x$),简化方程。
- 积分求解,并利用初始条件确定常数。
破题关键点:
- 识别方程中的全微分项 $x \, d(y \ln x)$,将原方程转化为可直接积分的形式。
- 正确应用积分技巧,特别是对 $\frac{\ln x}{x} \, dx$ 的积分。
步骤1:整理方程
原方程为:
$x \ln x \, dy + (y - \ln x) \, dx = 0$
将方程拆分为两部分:
$x \ln x \, dy + y \, dx - \ln x \, dx = 0$
步骤2:识别全微分项
注意到 $x \ln x \, dy + y \, dx$ 可表示为:
$x \, d(y \ln x) = x \left( \ln x \, dy + \frac{y}{x} \, dx \right) = x \ln x \, dy + y \, dx$
因此,原方程可改写为:
$x \, d(y \ln x) - \ln x \, dx = 0$
步骤3:分离变量并积分
整理得:
$x \, d(y \ln x) = \ln x \, dx$
两边除以 $x$:
$d(y \ln x) = \frac{\ln x}{x} \, dx$
对两边积分:
$y \ln x = \int \frac{\ln x}{x} \, dx$
步骤4:计算积分
令 $u = (\ln x)^2$,则 $du = 2 \ln x \cdot \frac{1}{x} \, dx$,积分得:
$\int \frac{\ln x}{x} \, dx = \frac{1}{2} (\ln x)^2 + C$
步骤5:代入初始条件
当 $x = e$ 时,$\ln e = 1$,代入方程:
$y \cdot 1 = \frac{1}{2} \cdot 1^2 + C \implies y = \frac{1}{2} + C$
根据题目条件(假设此处隐含 $y(e) = 1$),解得 $C = \frac{1}{2}$。