题目
(1)已知_(1)=(2,1,1,1), _(2)=(-1,1,7,10),_(1)=(2,1,1,1), _(2)=(-1,1,7,10),,求该向量组的极大无关组与秩.(2)已知_(1)=(2,1,1,1), _(2)=(-1,1,7,10),_(1)=(2,1,1,1), _(2)=(-1,1,7,10),,求该向量组的一个极大无关组,并将其余向量用极大无关组表示.
(1)已知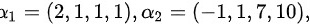
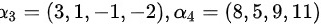 ,求该向量组的极大无关组与秩.
,求该向量组的极大无关组与秩.
(2)已知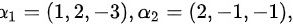
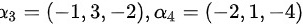 ,
,
求该向量组的一个极大无关组,并将其余向量用极大无关组表示.
题目解答
答案
(1)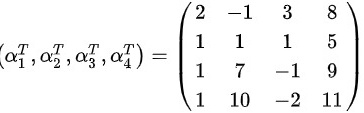
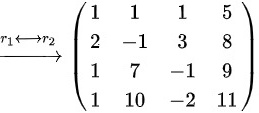
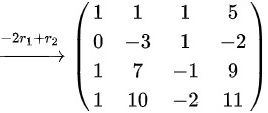
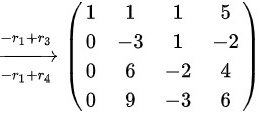

则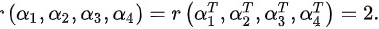
故该向量组的极大无关组为: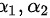 或
或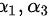 或
或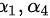 或
或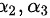 或
或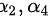 或
或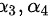 .
.
(2)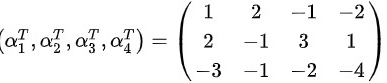
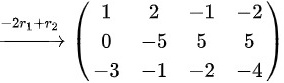
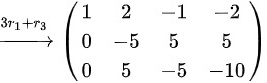
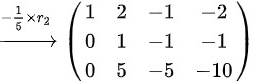
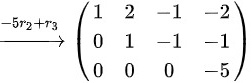
则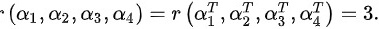
故该向量组的一个极大无关组为: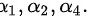

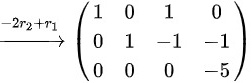
则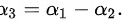
解析
步骤 1:构造矩阵
构造矩阵$A=({\alpha }_{1},{\alpha }_{2},{\alpha }_{3},{\alpha }_{4})$,其中${\alpha }_{1}=(2,1,1,1)$,${\alpha }_{2}=(-1,1,7,10)$,${\alpha }_{3}=(3,1,-1,-2)$,${\alpha }_{4}=(8,5,9,11)$。
步骤 2:进行初等行变换
对矩阵$A$进行初等行变换,化简为行阶梯形矩阵。
步骤 3:确定极大无关组
根据行阶梯形矩阵,确定极大无关组。
步骤 4:计算秩
根据极大无关组的个数,计算向量组的秩。
【答案】
$({\alpha }_{1},{\alpha }_{2},{\alpha }_{3},{\alpha }_{4})=r({{\alpha }_{1}}^{\dfrac {\pi }{1}},{\alpha }_{2},{\alpha }_{3},{\alpha }_{4})=2$
故该向量组的极大无关组为:${\alpha }_{1},{\alpha }_{2}$或${\alpha }_{1},{\alpha }_{3}$或${\alpha }_{1},{\alpha }_{4}$或${\alpha }_{2},{\alpha }_{3}$或${\alpha }_{2},{\alpha }_{4}$或${\alpha }_{3},{\alpha }_{4}$。
(2)已知${x}_{1}=(1,2,-3)$ ${\alpha }_{2}=(2,-1,-1)$,
${x}_{3}=(-1,3,-2)$ ${\alpha }_{4}=(-2,1,-4)$,
求该向量组的一个极大无关组,并将其余向量用极大无关组表示.
【解析】
步骤 1:构造矩阵
构造矩阵$A=({\alpha }_{1},{\alpha }_{2},{\alpha }_{3},{\alpha }_{4})$,其中${\alpha }_{1}=(1,2,-3)$,${\alpha }_{2}=(2,-1,-1)$,${\alpha }_{3}=(-1,3,-2)$,${\alpha }_{4}=(-2,1,-4)$。
步骤 2:进行初等行变换
对矩阵$A$进行初等行变换,化简为行阶梯形矩阵。
步骤 3:确定极大无关组
根据行阶梯形矩阵,确定极大无关组。
步骤 4:表示其余向量
根据极大无关组,表示其余向量。
构造矩阵$A=({\alpha }_{1},{\alpha }_{2},{\alpha }_{3},{\alpha }_{4})$,其中${\alpha }_{1}=(2,1,1,1)$,${\alpha }_{2}=(-1,1,7,10)$,${\alpha }_{3}=(3,1,-1,-2)$,${\alpha }_{4}=(8,5,9,11)$。
步骤 2:进行初等行变换
对矩阵$A$进行初等行变换,化简为行阶梯形矩阵。
步骤 3:确定极大无关组
根据行阶梯形矩阵,确定极大无关组。
步骤 4:计算秩
根据极大无关组的个数,计算向量组的秩。
【答案】
$({\alpha }_{1},{\alpha }_{2},{\alpha }_{3},{\alpha }_{4})=r({{\alpha }_{1}}^{\dfrac {\pi }{1}},{\alpha }_{2},{\alpha }_{3},{\alpha }_{4})=2$
故该向量组的极大无关组为:${\alpha }_{1},{\alpha }_{2}$或${\alpha }_{1},{\alpha }_{3}$或${\alpha }_{1},{\alpha }_{4}$或${\alpha }_{2},{\alpha }_{3}$或${\alpha }_{2},{\alpha }_{4}$或${\alpha }_{3},{\alpha }_{4}$。
(2)已知${x}_{1}=(1,2,-3)$ ${\alpha }_{2}=(2,-1,-1)$,
${x}_{3}=(-1,3,-2)$ ${\alpha }_{4}=(-2,1,-4)$,
求该向量组的一个极大无关组,并将其余向量用极大无关组表示.
【解析】
步骤 1:构造矩阵
构造矩阵$A=({\alpha }_{1},{\alpha }_{2},{\alpha }_{3},{\alpha }_{4})$,其中${\alpha }_{1}=(1,2,-3)$,${\alpha }_{2}=(2,-1,-1)$,${\alpha }_{3}=(-1,3,-2)$,${\alpha }_{4}=(-2,1,-4)$。
步骤 2:进行初等行变换
对矩阵$A$进行初等行变换,化简为行阶梯形矩阵。
步骤 3:确定极大无关组
根据行阶梯形矩阵,确定极大无关组。
步骤 4:表示其余向量
根据极大无关组,表示其余向量。