题目
设 f(x)= )^2f(x-1)dx,
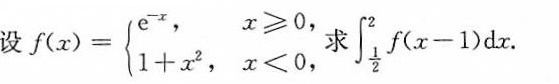
题目解答
答案
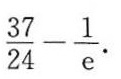
解析
步骤 1:确定积分区间
给定的积分区间是 $\dfrac{1}{2}$ 到 $2$,我们需要计算 $f(x-1)$ 在这个区间上的积分。首先,我们需要确定 $x-1$ 在这个区间上的取值范围。当 $x=\dfrac{1}{2}$ 时,$x-1=-\dfrac{1}{2}$;当 $x=2$ 时,$x-1=1$。因此,$x-1$ 的取值范围是 $-\dfrac{1}{2}$ 到 $1$。
步骤 2:分段计算积分
根据 $f(x)$ 的定义,我们需要分段计算积分。当 $x-1\geqslant 0$,即 $x\geqslant 1$ 时,$f(x-1)={e}^{-(x-1)}$;当 $x-1<0$,即 $x<1$ 时,$f(x-1)=1+(x-1)^2$。因此,我们需要将积分区间 $\dfrac{1}{2}$ 到 $2$ 分成两部分:$\dfrac{1}{2}$ 到 $1$ 和 $1$ 到 $2$。
步骤 3:计算积分
在区间 $\dfrac{1}{2}$ 到 $1$ 上,$f(x-1)=1+(x-1)^2$,因此积分是 ${\int }_{\dfrac{1}{2}}^{1}(1+(x-1)^2)dx$。在区间 $1$ 到 $2$ 上,$f(x-1)={e}^{-(x-1)}$,因此积分是 ${\int }_{1}^{2}{e}^{-(x-1)}dx$。将这两个积分相加,得到最终结果。
给定的积分区间是 $\dfrac{1}{2}$ 到 $2$,我们需要计算 $f(x-1)$ 在这个区间上的积分。首先,我们需要确定 $x-1$ 在这个区间上的取值范围。当 $x=\dfrac{1}{2}$ 时,$x-1=-\dfrac{1}{2}$;当 $x=2$ 时,$x-1=1$。因此,$x-1$ 的取值范围是 $-\dfrac{1}{2}$ 到 $1$。
步骤 2:分段计算积分
根据 $f(x)$ 的定义,我们需要分段计算积分。当 $x-1\geqslant 0$,即 $x\geqslant 1$ 时,$f(x-1)={e}^{-(x-1)}$;当 $x-1<0$,即 $x<1$ 时,$f(x-1)=1+(x-1)^2$。因此,我们需要将积分区间 $\dfrac{1}{2}$ 到 $2$ 分成两部分:$\dfrac{1}{2}$ 到 $1$ 和 $1$ 到 $2$。
步骤 3:计算积分
在区间 $\dfrac{1}{2}$ 到 $1$ 上,$f(x-1)=1+(x-1)^2$,因此积分是 ${\int }_{\dfrac{1}{2}}^{1}(1+(x-1)^2)dx$。在区间 $1$ 到 $2$ 上,$f(x-1)={e}^{-(x-1)}$,因此积分是 ${\int }_{1}^{2}{e}^{-(x-1)}dx$。将这两个积分相加,得到最终结果。