题目
[题目]指出下列函数中哪些是偶函数,哪些是奇-|||-函数,哪些既非偶函数又非奇函数?-|||-(1) =(x)^2(1-(x)^2);-|||-(2) =3(x)^2-(x)^3;-|||-(3) =dfrac (1-{x)^2}(1+{x)^2};-|||-(4) =x(x-1)(x+1);-|||-(5) =sin x-cos x+1;-|||-(6) =dfrac ({a)^x+(a)^-x}(2)

题目解答
答案
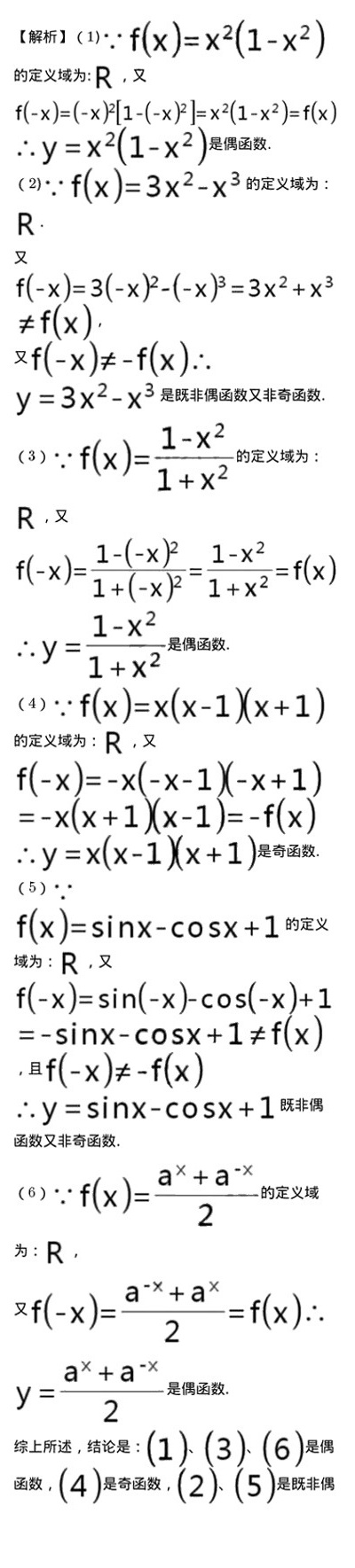
解析
奇偶函数的判断核心在于验证$f(-x)$与$f(x)$的关系:
- 偶函数:$f(-x) = f(x)$,图像关于$y$轴对称;
- 奇函数:$f(-x) = -f(x)$,图像关于原点对称;
- 非奇非偶:两者均不满足。
关键步骤:
- 确定定义域是否关于原点对称(若不对称,直接非奇非偶);
- 计算$f(-x)$,化简并与$f(x)$比较;
- 判断类型,根据等式关系分类。
(1)$y = x^2(1 - x^2)$
- 定义域:全体实数$R$;
- 计算$f(-x)$:
$f(-x) = (-x)^2[1 - (-x)^2] = x^2(1 - x^2) = f(x)$ - 结论:偶函数。
(2)$y = 3x^2 - x^3$
- 定义域:全体实数$R$;
- 计算$f(-x)$:
$f(-x) = 3(-x)^2 - (-x)^3 = 3x^2 + x^3$ - 比较:$f(-x) \neq f(x)$且$f(-x) \neq -f(x)$;
- 结论:既非偶函数又非奇函数。
(3)$y = \dfrac{1 - x^2}{1 + x^2}$
- 定义域:全体实数$R$;
- 计算$f(-x)$:
$f(-x) = \dfrac{1 - (-x)^2}{1 + (-x)^2} = \dfrac{1 - x^2}{1 + x^2} = f(x)$ - 结论:偶函数。
(4)$y = x(x - 1)(x + 1)$
- 展开:$y = x(x^2 - 1) = x^3 - x$;
- 计算$f(-x)$:
$f(-x) = (-x)[(-x)^2 - 1] = -x(x^2 - 1) = -x^3 + x = -f(x)$ - 结论:奇函数。
(5)$y = \sin x - \cos x + 1$
- 计算$f(-x)$:
$f(-x) = \sin(-x) - \cos(-x) + 1 = -\sin x - \cos x + 1$ - 比较:$f(-x) \neq f(x)$且$f(-x) \neq -f(x)$;
- 结论:既非偶函数又非奇函数。
(6)$y = \dfrac{a^x + a^{-x}}{2}$
- 定义域:全体实数$R$;
- 计算$f(-x)$:
$f(-x) = \dfrac{a^{-x} + a^x}{2} = \dfrac{a^x + a^{-x}}{2} = f(x)$ - 结论:偶函数。