题目
已知随机变量X的密度函数为(x)= ) c,-1leqslant xleqslant 1 0, .试求常数c,并求出X的分布函数。
已知随机变量X的密度函数为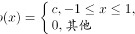 试求常数c,并求出X的分布函数。
试求常数c,并求出X的分布函数。
题目解答
答案
由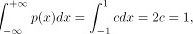 得
得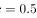 ,利用分段积分,可求出
,利用分段积分,可求出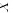 的分布函数:当
的分布函数:当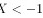 时,
时,
当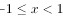 时,
时,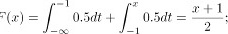
当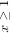 时,
时,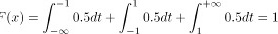
所以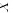 的分布函数为
的分布函数为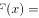

解析
步骤 1:确定常数c
根据概率密度函数的性质,整个定义域上的积分应等于1。因此,我们有:
$$\int_{-\infty}^{\infty} p(x) dx = 1$$
由于p(x)在-1到1之间为c,其他地方为0,所以积分可以简化为:
$$\int_{-1}^{1} c dx = 1$$
步骤 2:计算积分
计算上述积分,我们得到:
$$c \int_{-1}^{1} dx = c[x]_{-1}^{1} = c(1 - (-1)) = 2c$$
步骤 3:求解c
根据步骤2的结果,我们有:
$$2c = 1$$
解得:
$$c = \frac{1}{2}$$
步骤 4:求分布函数
分布函数F(x)定义为从负无穷到x的积分,即:
$$F(x) = \int_{-\infty}^{x} p(t) dt$$
根据p(x)的定义,我们可以分段求解F(x):
- 当$x < -1$时,$F(x) = 0$
- 当$-1 \leq x < 1$时,$F(x) = \int_{-1}^{x} \frac{1}{2} dt = \frac{1}{2}[t]_{-1}^{x} = \frac{x + 1}{2}$
- 当$x \geq 1$时,$F(x) = 1$
根据概率密度函数的性质,整个定义域上的积分应等于1。因此,我们有:
$$\int_{-\infty}^{\infty} p(x) dx = 1$$
由于p(x)在-1到1之间为c,其他地方为0,所以积分可以简化为:
$$\int_{-1}^{1} c dx = 1$$
步骤 2:计算积分
计算上述积分,我们得到:
$$c \int_{-1}^{1} dx = c[x]_{-1}^{1} = c(1 - (-1)) = 2c$$
步骤 3:求解c
根据步骤2的结果,我们有:
$$2c = 1$$
解得:
$$c = \frac{1}{2}$$
步骤 4:求分布函数
分布函数F(x)定义为从负无穷到x的积分,即:
$$F(x) = \int_{-\infty}^{x} p(t) dt$$
根据p(x)的定义,我们可以分段求解F(x):
- 当$x < -1$时,$F(x) = 0$
- 当$-1 \leq x < 1$时,$F(x) = \int_{-1}^{x} \frac{1}{2} dt = \frac{1}{2}[t]_{-1}^{x} = \frac{x + 1}{2}$
- 当$x \geq 1$时,$F(x) = 1$