题目
若f(x)在f(x)上连续,则f(x)( )A. 不一定存在B. 一定不存在C. 必定存在D. 以上都不正确
若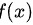 在
在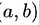 上连续,则
上连续,则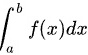 ( )
( )
A. 不一定存在
B. 一定不存在
C. 必定存在
D. 以上都不正确
题目解答
答案
解:若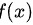 在
在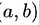 上连续
上连续
根据函数连续必可积可知: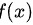 在
在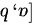 上连续,则
上连续,则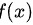 在
在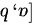 上可积,则
上可积,则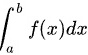 存在,
存在,
因为无法确定 ,
, 两点的情况,当
两点的情况,当 ,
, 有一个为函数的间断点时,积分
有一个为函数的间断点时,积分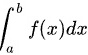 不存在,
不存在,
所以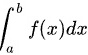 不一定存在.
不一定存在.
故答案为:A.
解析
步骤 1:理解函数连续与可积的关系
函数在某区间上连续,意味着该函数在该区间上没有间断点,即函数在该区间上是光滑的。根据数学分析中的定理,如果一个函数在闭区间上连续,那么该函数在该闭区间上可积。这意味着,如果函数在闭区间上连续,那么该函数在该闭区间上的定积分存在。
步骤 2:分析题目中的条件
题目中给出的条件是函数f(x)在开区间(a,b)上连续。这意味着函数f(x)在(a,b)上没有间断点,但题目没有给出关于端点a和b的信息。因此,我们不能确定函数f(x)在端点a和b处是否连续。
步骤 3:考虑端点的情况
如果函数f(x)在端点a和b处连续,那么函数f(x)在闭区间[a,b]上连续,根据步骤1中的定理,函数f(x)在闭区间[a,b]上可积,即${\int }_{a}^{b}f(x)dx$存在。然而,如果函数f(x)在端点a或b处不连续,那么函数f(x)在闭区间[a,b]上不可积,即${\int }_{a}^{b}f(x)dx$不存在。
函数在某区间上连续,意味着该函数在该区间上没有间断点,即函数在该区间上是光滑的。根据数学分析中的定理,如果一个函数在闭区间上连续,那么该函数在该闭区间上可积。这意味着,如果函数在闭区间上连续,那么该函数在该闭区间上的定积分存在。
步骤 2:分析题目中的条件
题目中给出的条件是函数f(x)在开区间(a,b)上连续。这意味着函数f(x)在(a,b)上没有间断点,但题目没有给出关于端点a和b的信息。因此,我们不能确定函数f(x)在端点a和b处是否连续。
步骤 3:考虑端点的情况
如果函数f(x)在端点a和b处连续,那么函数f(x)在闭区间[a,b]上连续,根据步骤1中的定理,函数f(x)在闭区间[a,b]上可积,即${\int }_{a}^{b}f(x)dx$存在。然而,如果函数f(x)在端点a或b处不连续,那么函数f(x)在闭区间[a,b]上不可积,即${\int }_{a}^{b}f(x)dx$不存在。