题目
设长方形的长K~U(0,1),已知长方形的周长为2,求长方形面积的数学期望和方差。
设长方形的长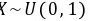 ,已知长方形的周长为2,求长方形面积的数学期望和方差。
,已知长方形的周长为2,求长方形面积的数学期望和方差。
题目解答
答案
解:因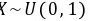 ,故
,故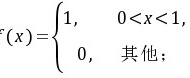 ……………………(1分)
……………………(1分)
面积为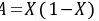 ,所以
,所以
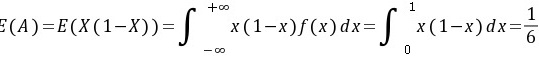 …………(2分)
…………(2分)
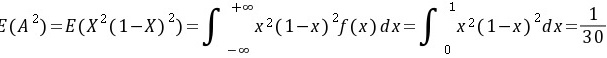 ,
,
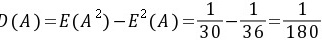 …………………………(3分)
…………………………(3分)
解析
步骤 1:确定长方形的长和宽
已知长方形的周长为2,设长方形的长为$X$,宽为$Y$,则有$2(X+Y)=2$,即$X+Y=1$。由于$X\sim U(0,1)$,则$Y=1-X$。
步骤 2:计算长方形面积的数学期望
长方形的面积$A=X(1-X)$,则$E(A)=E(X(1-X))$。由于$X\sim U(0,1)$,则$E(X)=\frac{1}{2}$,$E(X^2)=\int_{0}^{1}x^2dx=\frac{1}{3}$。因此,$E(A)=E(X)-E(X^2)=\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$。
步骤 3:计算长方形面积的方差
$D(A)=E(A^2)-E^2(A)$。首先计算$E(A^2)=E(X^2(1-X)^2)$,由于$X\sim U(0,1)$,则$E(X^2(1-X)^2)=\int_{0}^{1}x^2(1-x)^2dx=\frac{1}{30}$。因此,$D(A)=\frac{1}{30}-\frac{1}{36}=\frac{1}{180}$。
已知长方形的周长为2,设长方形的长为$X$,宽为$Y$,则有$2(X+Y)=2$,即$X+Y=1$。由于$X\sim U(0,1)$,则$Y=1-X$。
步骤 2:计算长方形面积的数学期望
长方形的面积$A=X(1-X)$,则$E(A)=E(X(1-X))$。由于$X\sim U(0,1)$,则$E(X)=\frac{1}{2}$,$E(X^2)=\int_{0}^{1}x^2dx=\frac{1}{3}$。因此,$E(A)=E(X)-E(X^2)=\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$。
步骤 3:计算长方形面积的方差
$D(A)=E(A^2)-E^2(A)$。首先计算$E(A^2)=E(X^2(1-X)^2)$,由于$X\sim U(0,1)$,则$E(X^2(1-X)^2)=\int_{0}^{1}x^2(1-x)^2dx=\frac{1}{30}$。因此,$D(A)=\frac{1}{30}-\frac{1}{36}=\frac{1}{180}$。