题目
设f(x)= ^2)},xneq 0 0, x=0 . 求f(n)(0)。
设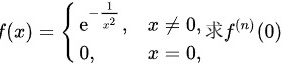 。
。
题目解答
答案
对于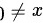 ,有
,有
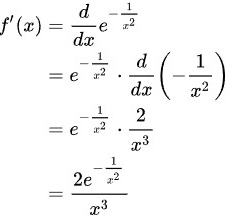
由此可知,当 为正整数时,
为正整数时,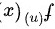 可表示为
可表示为 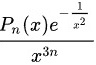 的形式,其中
的形式,其中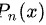 为关于
为关于 的一个多项式。
的一个多项式。
当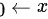 时,
时,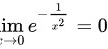 ,所以
,所以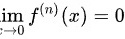 。
。
因此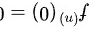 。
。
解析
考查要点:本题主要考查高阶导数在特定点的计算,涉及极限的性质和导数定义的应用,同时隐含对光滑非解析函数性质的理解。
解题核心思路:
- 分析导数表达式结构:题目中给出的n阶导数形式为$\dfrac{P_n(x)e^{-1/x^2}}{x^{3n}}$,需判断其在$x \to 0$时的极限。
- 比较指数函数与多项式的衰减/增长速度:$e^{-1/x^2}$的衰减速度远快于任何多项式分式$\dfrac{1}{x^{3n}}$的增长,因此整体极限为0。
- 导数定义与极限关系:通过极限$\lim_{x \to 0} f^{(n)}(x) = 0$,结合导数在$x=0$处的连续性,得出$f^{(n)}(0) = 0$。
步骤1:分析导数表达式
当$x \neq 0$时,$f^{(n)}(x) = \dfrac{P_n(x)e^{-1/x^2}}{x^{3n}}$,其中$P_n(x)$是关于$x$的多项式。
步骤2:计算极限$\lim_{x \to 0} f^{(n)}(x)$
- 指数项的极限:$\lim_{x \to 0} e^{-1/x^2} = 0$,因为当$x \to 0$时,$-1/x^2 \to -\infty$,指数函数趋近于0。
- 分式的极限:$\lim_{x \to 0} \dfrac{P_n(x)}{x^{3n}}$中,$P_n(x)$在$x \to 0$时可能趋近于常数或0,但分母$x^{3n} \to 0$,分式本身可能发散。
- 整体极限:尽管分式发散,但$e^{-1/x^2}$的衰减速度远快于分式的发散速度,因此整体极限为0:
$\lim_{x \to 0} \dfrac{P_n(x)e^{-1/x^2}}{x^{3n}} = 0.$
步骤3:确定$f^{(n)}(0)$的值
根据导数的连续性,若$\lim_{x \to 0} f^{(n)}(x) = 0$,则$f^{(n)}(0) = 0$。