题目
[例5](2020,数三)函数 (x)=dfrac (eln |1+x|)(({e)^x-1)(x-2)} 的第二类间断点的个数为-|||-(A)1. (B)2. (C)3. (D)4.
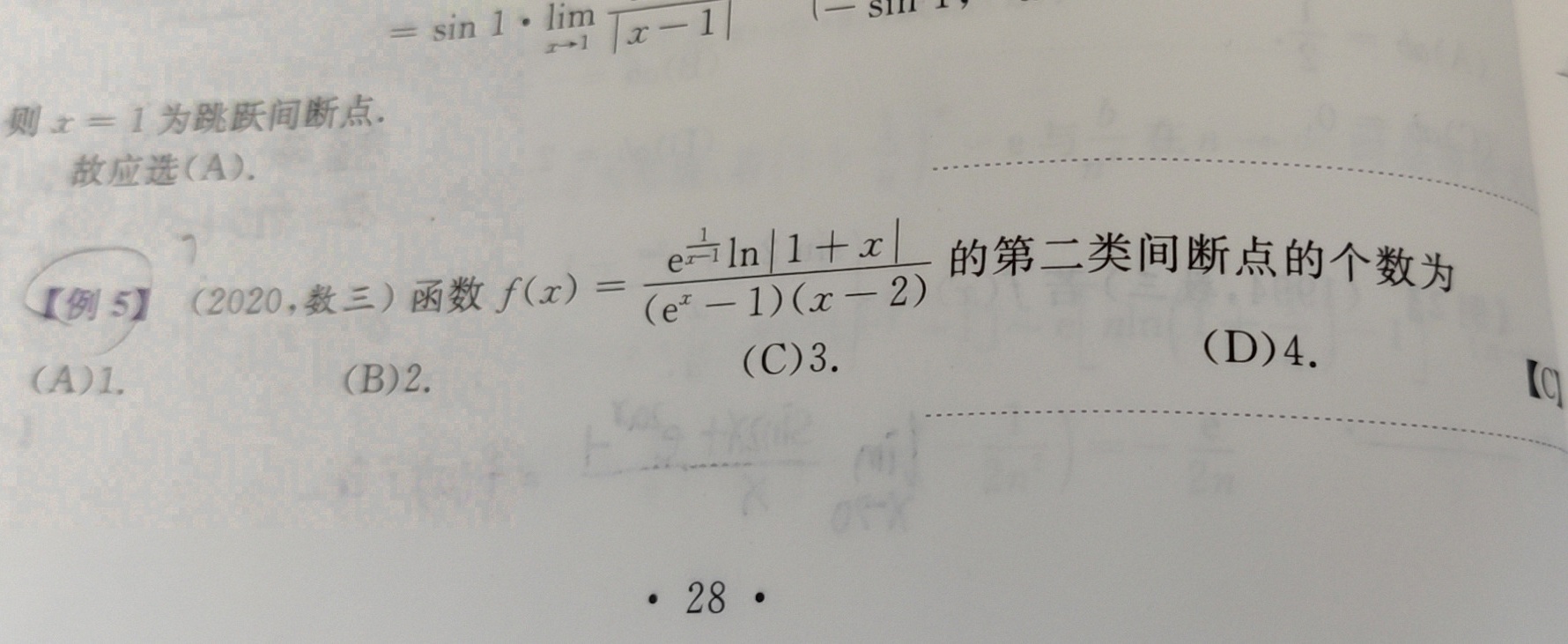
题目解答
答案

解析
步骤 1:确定函数的定义域
函数 $f(x)=\dfrac {{e}^{\dfrac {1}{x-1}\ln |1+x|}}{({e}^{x}-1)(x-2)}$ 的定义域需要满足分母不为零,即 $({e}^{x}-1)(x-2)\neq 0$,同时分子中的对数函数 $\ln |1+x|$ 需要满足 $|1+x|\neq 0$。因此,定义域为 $x\neq 0, 1, 2$ 且 $x\neq -1$。
步骤 2:分析间断点
根据定义域,函数的间断点为 $x=-1, 0, 1, 2$。我们需要进一步分析这些点是第一类间断点还是第二类间断点。
- 对于 $x=-1$,分子中的 $\ln |1+x|$ 在 $x=-1$ 时为 $\ln 0$,是未定义的,因此 $x=-1$ 是第二类间断点。
- 对于 $x=0$,分子中的 $\ln |1+x|$ 在 $x=0$ 时为 $\ln 1=0$,而分母中的 $({e}^{x}-1)$ 在 $x=0$ 时为 $0$,因此 $x=0$ 是第一类间断点。
- 对于 $x=1$,分子中的 $\ln |1+x|$ 在 $x=1$ 时为 $\ln 2$,而分母中的 $({e}^{x}-1)$ 在 $x=1$ 时为 $e-1$,因此 $x=1$ 是第二类间断点。
- 对于 $x=2$,分子中的 $\ln |1+x|$ 在 $x=2$ 时为 $\ln 3$,而分母中的 $(x-2)$ 在 $x=2$ 时为 $0$,因此 $x=2$ 是第二类间断点。
步骤 3:总结
根据上述分析,函数 $f(x)$ 的第二类间断点有 $x=-1, 1, 2$,共3个。
函数 $f(x)=\dfrac {{e}^{\dfrac {1}{x-1}\ln |1+x|}}{({e}^{x}-1)(x-2)}$ 的定义域需要满足分母不为零,即 $({e}^{x}-1)(x-2)\neq 0$,同时分子中的对数函数 $\ln |1+x|$ 需要满足 $|1+x|\neq 0$。因此,定义域为 $x\neq 0, 1, 2$ 且 $x\neq -1$。
步骤 2:分析间断点
根据定义域,函数的间断点为 $x=-1, 0, 1, 2$。我们需要进一步分析这些点是第一类间断点还是第二类间断点。
- 对于 $x=-1$,分子中的 $\ln |1+x|$ 在 $x=-1$ 时为 $\ln 0$,是未定义的,因此 $x=-1$ 是第二类间断点。
- 对于 $x=0$,分子中的 $\ln |1+x|$ 在 $x=0$ 时为 $\ln 1=0$,而分母中的 $({e}^{x}-1)$ 在 $x=0$ 时为 $0$,因此 $x=0$ 是第一类间断点。
- 对于 $x=1$,分子中的 $\ln |1+x|$ 在 $x=1$ 时为 $\ln 2$,而分母中的 $({e}^{x}-1)$ 在 $x=1$ 时为 $e-1$,因此 $x=1$ 是第二类间断点。
- 对于 $x=2$,分子中的 $\ln |1+x|$ 在 $x=2$ 时为 $\ln 3$,而分母中的 $(x-2)$ 在 $x=2$ 时为 $0$,因此 $x=2$ 是第二类间断点。
步骤 3:总结
根据上述分析,函数 $f(x)$ 的第二类间断点有 $x=-1, 1, 2$,共3个。