题目
计算iint ln (1+(x)^2+(y)^2)do,其中D是由圆周iint ln (1+(x)^2+(y)^2)do及坐标轴所围成的在第一象限内的闭区域.
计算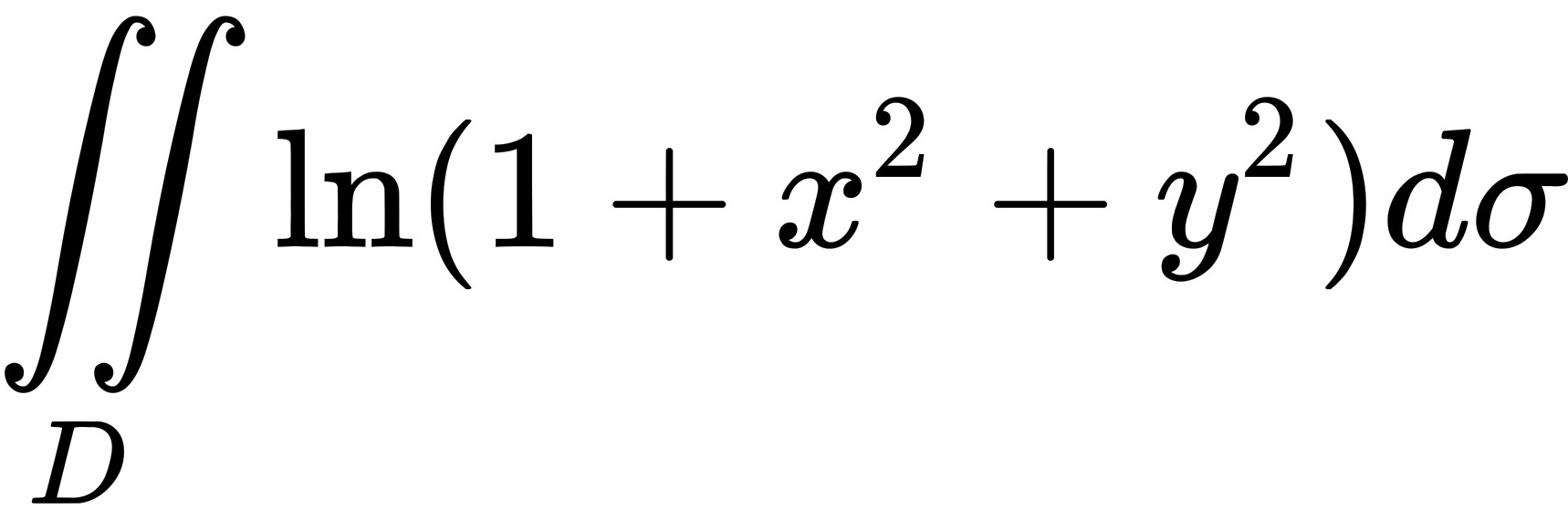 ,其中D是由圆周
,其中D是由圆周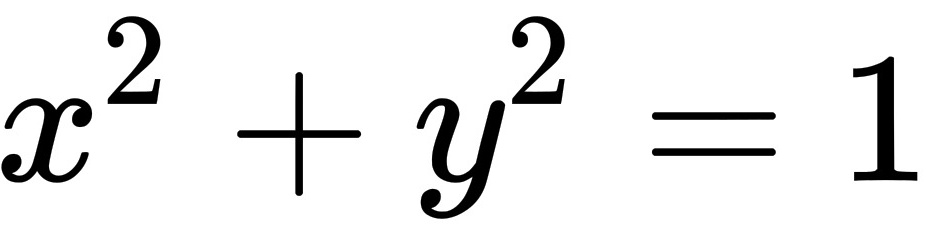 及坐标轴所围成的在第一象限内的闭区域.
及坐标轴所围成的在第一象限内的闭区域.
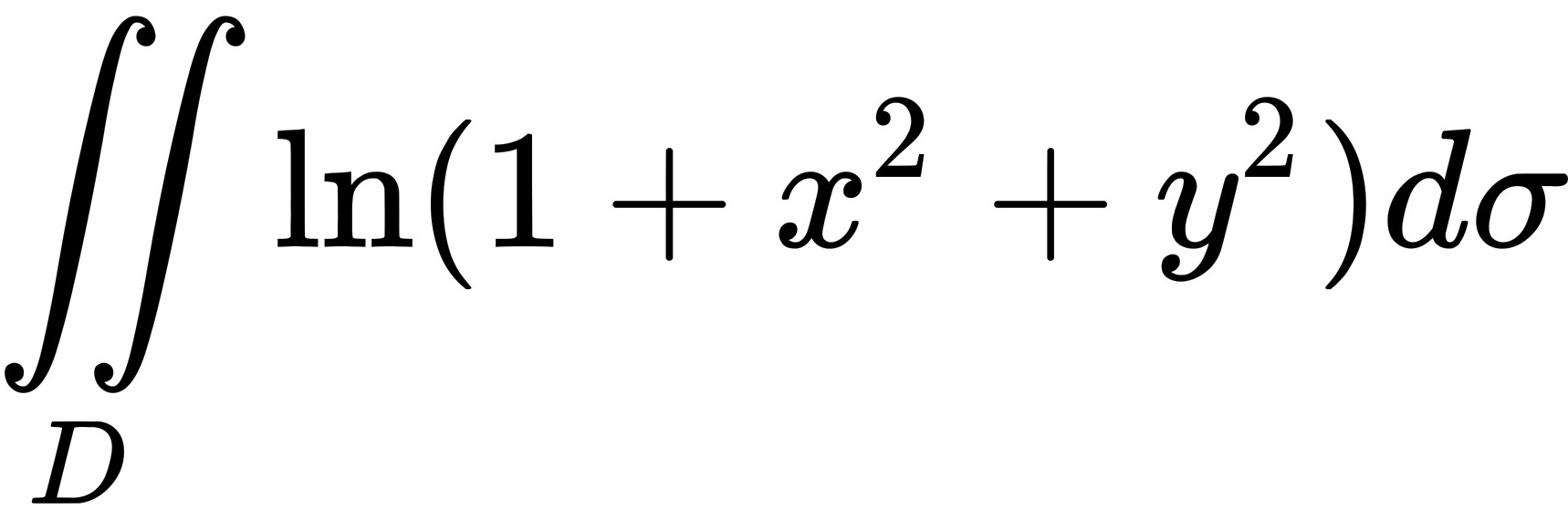 ,其中D是由圆周
,其中D是由圆周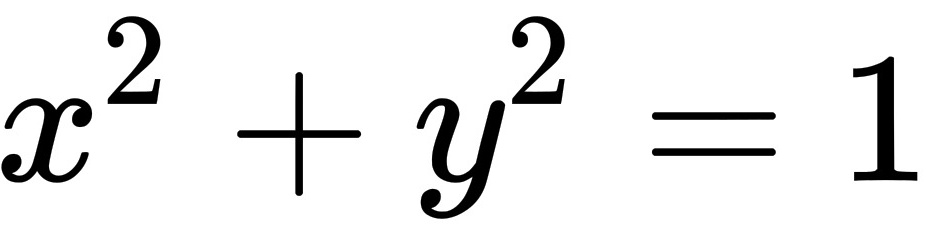 及坐标轴所围成的在第一象限内的闭区域.
及坐标轴所围成的在第一象限内的闭区域.题目解答
答案
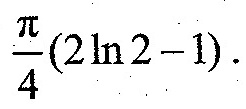
解析
步骤 1:确定积分区域
积分区域D是由圆周${x}^{2}+{y}^{2}=1$及坐标轴所围成的在第一象限内的闭区域。这意味着x和y的取值范围都是从0到1,且满足${x}^{2}+{y}^{2}\leq 1$。
步骤 2:转换为极坐标
为了简化积分,我们使用极坐标变换。设$x=r\cos\theta$,$y=r\sin\theta$,则${x}^{2}+{y}^{2}=r^2$。积分区域D在极坐标下变为$0\leq r\leq 1$,$0\leq \theta\leq \frac{\pi}{2}$。积分元素$do$在极坐标下变为$rdrd\theta$。
步骤 3:计算积分
将原积分转换为极坐标下的形式,得到
$$\int_{0}^{\frac{\pi}{2}}\int_{0}^{1}\ln(1+r^2)rdrd\theta$$
首先对$r$积分,然后对$\theta$积分。对$r$积分时,使用分部积分法,设$u=\ln(1+r^2)$,$dv=rdr$,则$du=\frac{2r}{1+r^2}dr$,$v=\frac{1}{2}r^2$。因此,
$$\int_{0}^{1}\ln(1+r^2)rdr=\left[\frac{1}{2}r^2\ln(1+r^2)\right]_{0}^{1}-\int_{0}^{1}\frac{r^3}{1+r^2}dr$$
$$=\frac{1}{2}\ln 2-\int_{0}^{1}\left(r-\frac{r}{1+r^2}\right)dr$$
$$=\frac{1}{2}\ln 2-\left[\frac{1}{2}r^2-\frac{1}{2}\ln(1+r^2)\right]_{0}^{1}$$
$$=\frac{1}{2}\ln 2-\frac{1}{2}+\frac{1}{2}\ln 2$$
$$=\ln 2-\frac{1}{2}$$
然后对$\theta$积分,得到
$$\int_{0}^{\frac{\pi}{2}}\left(\ln 2-\frac{1}{2}\right)d\theta=\left(\ln 2-\frac{1}{2}\right)\frac{\pi}{2}$$
$$=\frac{\pi}{4}(2\ln 2-1)$$
积分区域D是由圆周${x}^{2}+{y}^{2}=1$及坐标轴所围成的在第一象限内的闭区域。这意味着x和y的取值范围都是从0到1,且满足${x}^{2}+{y}^{2}\leq 1$。
步骤 2:转换为极坐标
为了简化积分,我们使用极坐标变换。设$x=r\cos\theta$,$y=r\sin\theta$,则${x}^{2}+{y}^{2}=r^2$。积分区域D在极坐标下变为$0\leq r\leq 1$,$0\leq \theta\leq \frac{\pi}{2}$。积分元素$do$在极坐标下变为$rdrd\theta$。
步骤 3:计算积分
将原积分转换为极坐标下的形式,得到
$$\int_{0}^{\frac{\pi}{2}}\int_{0}^{1}\ln(1+r^2)rdrd\theta$$
首先对$r$积分,然后对$\theta$积分。对$r$积分时,使用分部积分法,设$u=\ln(1+r^2)$,$dv=rdr$,则$du=\frac{2r}{1+r^2}dr$,$v=\frac{1}{2}r^2$。因此,
$$\int_{0}^{1}\ln(1+r^2)rdr=\left[\frac{1}{2}r^2\ln(1+r^2)\right]_{0}^{1}-\int_{0}^{1}\frac{r^3}{1+r^2}dr$$
$$=\frac{1}{2}\ln 2-\int_{0}^{1}\left(r-\frac{r}{1+r^2}\right)dr$$
$$=\frac{1}{2}\ln 2-\left[\frac{1}{2}r^2-\frac{1}{2}\ln(1+r^2)\right]_{0}^{1}$$
$$=\frac{1}{2}\ln 2-\frac{1}{2}+\frac{1}{2}\ln 2$$
$$=\ln 2-\frac{1}{2}$$
然后对$\theta$积分,得到
$$\int_{0}^{\frac{\pi}{2}}\left(\ln 2-\frac{1}{2}\right)d\theta=\left(\ln 2-\frac{1}{2}\right)\frac{\pi}{2}$$
$$=\frac{\pi}{4}(2\ln 2-1)$$