题目
设函数f(x)在 (-infty ,+infty ) 内单调有界,(xn)为数列,下列命题正确-|||-的是 () .-|||-(A)若(xn)收敛,则(f(xn))收敛 (B)若(xn)单调,则(f(xn))收敛-|||-(C)若(f(xn))收敛,则(xn)收敛 (D)若(f(xn))单调,则(xn)收敛

题目解答
答案
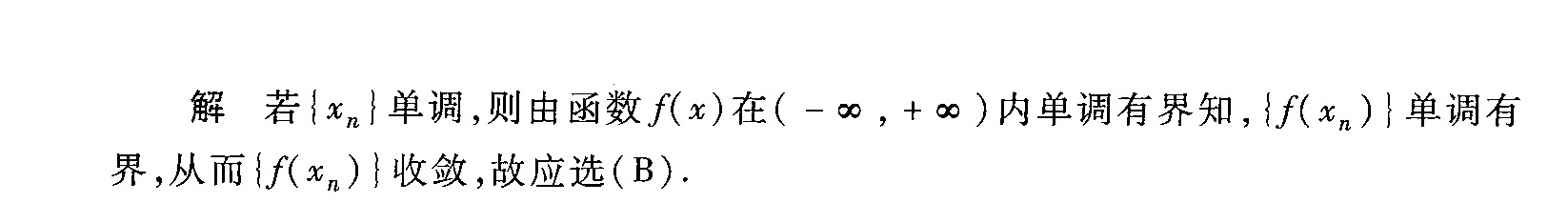
解析
考查要点:本题主要考查单调有界函数与数列收敛性的关系,需结合单调数列、复合函数收敛性等知识点进行分析。
解题核心思路:
- 抓住函数性质:函数$f(x)$在$\mathbb{R}$上单调有界,这意味着$f(x)$要么单调递增且有上界,要么单调递减且有下界。
- 分析数列与函数复合后的性质:当数列$\{x_n\}$具有某种特性(如收敛、单调)时,需判断$\{f(x_n)\}$是否保持对应性质(如收敛)。
- 反例排除法:对错误选项,可通过构造反例(如利用$f(x)$的不连续点或数列的特殊构造)说明其不成立。
破题关键点:
- 选项B的关键:若$\{x_n\}$单调,则$\{f(x_n)\}$因$f(x)$单调性而单调,再结合$f(x)$有界,可直接应用单调有界数列必收敛的定理。
- 其他选项的误区:需注意单调有界函数未必连续,且复合后的数列收敛性与原数列收敛性无必然联系。
选项分析
(A) 若$\{x_n\}$收敛,则$\{f(x_n)\}$收敛
错误。
- 反例:设$f(x)$在$x=0$处不连续,例如
$f(x) = \begin{cases} 0, & x < 0, \\ 1, & x \geq 0, \end{cases}$
取数列$x_n = (-1)^n \cdot \frac{1}{n}$,显然$x_n \to 0$,但$f(x_n)$在$0$和$1$之间震荡,不收敛。
(B) 若$\{x_n\}$单调,则$\{f(x_n)\}$收敛
正确。
- 推导:
- 若$\{x_n\}$单调递增,因$f(x)$单调,$\{f(x_n)\}$也单调(递增或递减)。
- $f(x)$有界,故$\{f(x_n)\}$单调有界,根据单调有界定理,必收敛。
(C) 若$\{f(x_n)\}$收敛,则$\{x_n\}$收敛
错误。
- 反例:设$f(x) = 1$(常数函数),则$\{f(x_n)\}$恒为$1$(收敛),但取$x_n = n$(发散数列),显然$\{x_n\}$不收敛。
(D) 若$\{f(x_n)\}$单调,则$\{x_n\}$收敛
错误。
- 反例:设$f(x) = \arctan x$(单调有界),取$x_n = n$,则$\{f(x_n)\}$单调递增且收敛于$\frac{\pi}{2}$,但$\{x_n\}$发散于$+\infty$。