题目
5.求点 (2,-1,2) 到平面 x+y-2z+1=0 的距离.
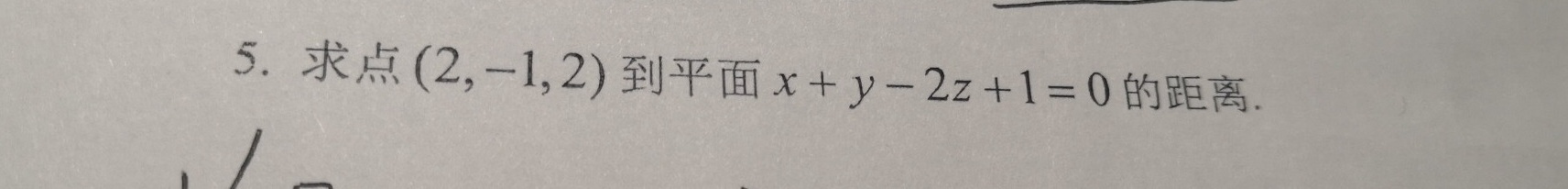
题目解答
答案

解析
步骤 1:确定点和平面的方程
点的坐标为 (2, -1, 2),平面的方程为 x + y - 2z + 1 = 0。
步骤 2:应用点到平面的距离公式
点到平面的距离公式为 $d = \dfrac{|Ax_0 + By_0 + Cz_0 + D|}{\sqrt{A^2 + B^2 + C^2}}$,其中 (x_0, y_0, z_0) 是点的坐标,A, B, C, D 是平面方程的系数。
步骤 3:代入点的坐标和平面的系数
将点 (2, -1, 2) 和平面 x + y - 2z + 1 = 0 的系数代入公式,得到 $d = \dfrac{|2 + (-1) - 2 \cdot 2 + 1|}{\sqrt{1^2 + 1^2 + (-2)^2}}$。
步骤 4:计算距离
计算得到 $d = \dfrac{|2 - 1 - 4 + 1|}{\sqrt{1 + 1 + 4}} = \dfrac{|-2|}{\sqrt{6}} = \dfrac{2}{\sqrt{6}} = \dfrac{2\sqrt{6}}{6} = \dfrac{\sqrt{6}}{3}$。
点的坐标为 (2, -1, 2),平面的方程为 x + y - 2z + 1 = 0。
步骤 2:应用点到平面的距离公式
点到平面的距离公式为 $d = \dfrac{|Ax_0 + By_0 + Cz_0 + D|}{\sqrt{A^2 + B^2 + C^2}}$,其中 (x_0, y_0, z_0) 是点的坐标,A, B, C, D 是平面方程的系数。
步骤 3:代入点的坐标和平面的系数
将点 (2, -1, 2) 和平面 x + y - 2z + 1 = 0 的系数代入公式,得到 $d = \dfrac{|2 + (-1) - 2 \cdot 2 + 1|}{\sqrt{1^2 + 1^2 + (-2)^2}}$。
步骤 4:计算距离
计算得到 $d = \dfrac{|2 - 1 - 4 + 1|}{\sqrt{1 + 1 + 4}} = \dfrac{|-2|}{\sqrt{6}} = \dfrac{2}{\sqrt{6}} = \dfrac{2\sqrt{6}}{6} = \dfrac{\sqrt{6}}{3}$。