题目
计算下列不定积分.-|||-int dfrac ({e)^x(1+xln x)}(x)dx

题目解答
答案
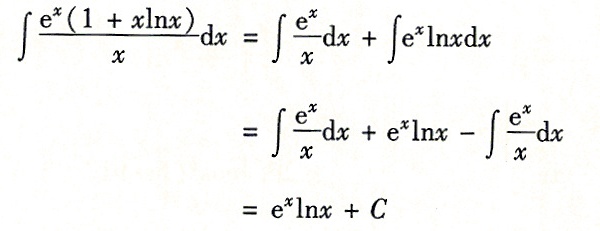
解析
步骤 1:将被积函数分解
将被积函数 $\dfrac {{e}^{x}(1+x\ln x)}{x}$ 分解为两个部分,即 $\dfrac {{e}^{x}}{x}$ 和 ${e}^{x}\ln x$,这样可以将原积分分解为两个积分的和。
步骤 2:计算第一个积分
计算 $\int \dfrac {{e}^{x}}{x}dx$,这个积分不能直接求出,但可以保留其形式。
步骤 3:计算第二个积分
计算 ${\int }_{{e}^{x}}\ln xdx$,使用分部积分法,设 $u=\ln x$,$dv={e}^{x}dx$,则 $du=\dfrac{1}{x}dx$,$v={e}^{x}$,根据分部积分公式 $\int udv=uv-\int vdu$,可以得到 ${\int }_{{e}^{x}}\ln xdx={e}^{x}\ln x-\int \dfrac {{e}^{x}}{x}dx$。
步骤 4:合并结果
将步骤 2 和步骤 3 的结果合并,得到原积分的解。
将被积函数 $\dfrac {{e}^{x}(1+x\ln x)}{x}$ 分解为两个部分,即 $\dfrac {{e}^{x}}{x}$ 和 ${e}^{x}\ln x$,这样可以将原积分分解为两个积分的和。
步骤 2:计算第一个积分
计算 $\int \dfrac {{e}^{x}}{x}dx$,这个积分不能直接求出,但可以保留其形式。
步骤 3:计算第二个积分
计算 ${\int }_{{e}^{x}}\ln xdx$,使用分部积分法,设 $u=\ln x$,$dv={e}^{x}dx$,则 $du=\dfrac{1}{x}dx$,$v={e}^{x}$,根据分部积分公式 $\int udv=uv-\int vdu$,可以得到 ${\int }_{{e}^{x}}\ln xdx={e}^{x}\ln x-\int \dfrac {{e}^{x}}{x}dx$。
步骤 4:合并结果
将步骤 2 和步骤 3 的结果合并,得到原积分的解。