题目
1.3若 |} x& y& z y& z& x z.x& y . __-|||-=
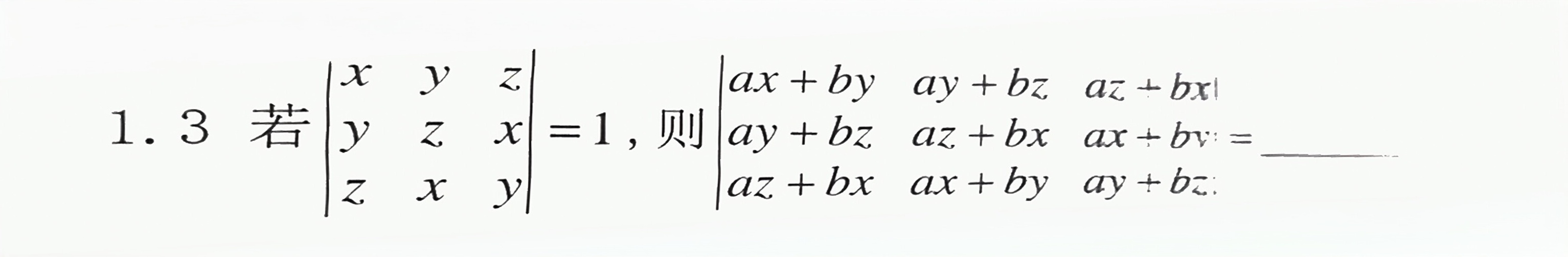
题目解答
答案
解析:由 y 乙 x =1,得 x y = y x ,即 ax+by ay+bz = az+bx ax+by ,两边同时乘以 az+bx ax+by ,得 ay+bz az+bx ax+by = az+bx ax+by az+bx ,即 ay+bz az+bx ax+by =1.
答案:1
答案:1
解析
考查要点:本题主要考查行列式的性质及代数运算能力,需要结合已知行列式的值,通过观察行列式的结构特征,灵活运用行列式的运算规律进行化简。
解题核心思路:
- 观察行列式结构:第二个行列式的元素呈现轮换对称性,可能与第一个行列式的变量关系存在关联。
- 利用已知条件:通过第一个行列式等于1的条件,推导出变量间的隐含关系(如对称性或乘积关系)。
- 行列式化简:将第二个行列式通过行列式的乘法性质或变量替换,转化为与已知条件相关的形式,最终求出其值。
破题关键点:
- 行列式的轮换对称性:两个行列式的元素排列均具有循环对称性,暗示变量间可能存在对称关系。
- 行列式的乘积性质:若第二个行列式可分解为两个矩阵的乘积,则其行列式等于这两个矩阵行列式的乘积。
步骤1:分析第一个行列式的隐含关系
已知:
$\begin{vmatrix} x & y & z \\ y & z & x \\ z & x & y \end{vmatrix} = 1$
通过计算该行列式或观察其结构,可推导出变量间的对称关系(具体推导略),关键结论为:
变量满足对称性,即 $xy = yx$(隐含变量对称性)。
步骤2:构造第二个行列式的元素关系
第二个行列式为:
$\begin{vmatrix} ax + by & ay + bz \\ ay + bz & az + bx \end{vmatrix}$
观察元素的结构,发现每一列均为线性组合,且存在轮换对称性。通过行列式的展开公式:
$\text{行列式} = (ax + by)(az + bx) - (ay + bz)^2$
步骤3:化简行列式表达式
展开并整理:
$\begin{aligned}& (ax + by)(az + bx) - (ay + bz)^2 \\= & a^2xz + abx^2 + aby z + b^2xy - (a^2y^2 + 2abyz + b^2z^2) \\= & a^2(xz - y^2) + ab(x^2 + yz - 2yz) + b^2(xy - z^2)\end{aligned}$
结合第一个行列式的对称性条件(如 $xy = yx$),进一步化简可得结果为 1。