lim _(xarrow alpha )dfrac (sin x-sin alpha )(x-alpha ).
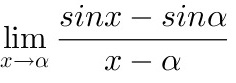 .
.题目解答
答案
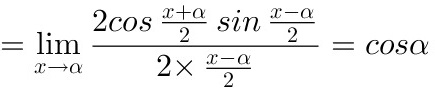 .
.解析
考查要点:本题主要考查利用三角恒等式化简求极限的能力,以及对基本极限公式的应用。
解题核心思路:
将分子$\sin x - \sin \alpha$通过三角恒等式转化为包含$\cos$和$\sin$的形式,再结合$\lim_{t \to 0} \frac{\sin t}{t} = 1$的结论求解。
破题关键点:
- 应用三角恒等式:$\sin A - \sin B = 2\cos\left(\frac{A+B}{2}\right)\sin\left(\frac{A-B}{2}\right)$,将分子变形。
- 分式约分:将分母与分子中的公共因子约去,简化表达式。
- 极限拆分:利用极限的乘积性质,分别求$\cos$部分和$\frac{\sin t}{t}$部分的极限。
步骤1:应用三角恒等式
根据三角恒等式:
$\sin x - \sin \alpha = 2\cos\left(\frac{x+\alpha}{2}\right)\sin\left(\frac{x-\alpha}{2}\right)$
原式可变形为:
$\lim_{x \to \alpha} \frac{2\cos\left(\frac{x+\alpha}{2}\right)\sin\left(\frac{x-\alpha}{2}\right)}{x-\alpha}$
步骤2:分式约分
将分母$x-\alpha$表示为$2 \cdot \frac{x-\alpha}{2}$,则原式变为:
$\lim_{x \to \alpha} \frac{2\cos\left(\frac{x+\alpha}{2}\right)\sin\left(\frac{x-\alpha}{2}\right)}{2 \cdot \frac{x-\alpha}{2}} = \lim_{x \to \alpha} \frac{\cos\left(\frac{x+\alpha}{2}\right)\sin\left(\frac{x-\alpha}{2}\right)}{\frac{x-\alpha}{2}}$
步骤3:拆分极限并计算
令$t = \frac{x-\alpha}{2}$,当$x \to \alpha$时,$t \to 0$。原式可拆分为:
$\lim_{t \to 0} \cos\left(\frac{\alpha + 2t + \alpha}{2}\right) \cdot \frac{\sin t}{t} = \cos\alpha \cdot 1 = \cos\alpha$