题目
求函数(x,y)=(6x-(x)^2)(4y-(y)^2)的极值
求函数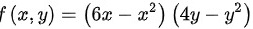 的极值
的极值
题目解答
答案
解:
先建立函数的偏导数方程组
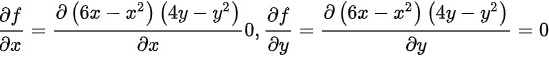
得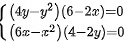
解得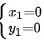
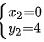
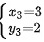
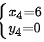
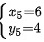
共五组解。得驻点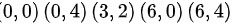
又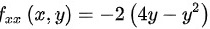
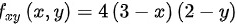
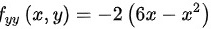
由判定极值的充分条件知:
在点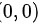 处,
处,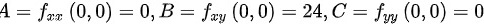
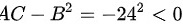 ,故
,故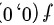 不是极值。
不是极值。
在点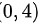 处,
处,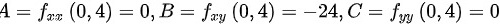
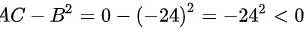 ,故
,故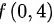 不是极值。
不是极值。
在点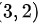 处,
处,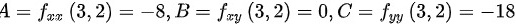
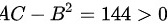 0" data-width="173" data-height="25" data-size="2180" data-format="png" style="max-width:100%">,故在点
0" data-width="173" data-height="25" data-size="2180" data-format="png" style="max-width:100%">,故在点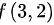 处取得极大值。极大值
处取得极大值。极大值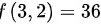
在点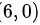 处,
处,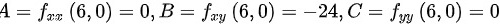
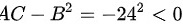 ,故
,故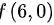 不是极值。
不是极值。
在点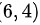 处,
处,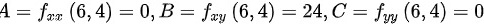
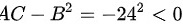 ,故
,故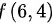 不是极值。
不是极值。
所以综上,函数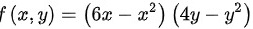 的极大值为
的极大值为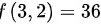
解析
步骤 1:求偏导数
首先,我们需要求出函数$f(x;y)=(6x-{x}^{2})(4y-{y}^{2})$关于$x$和$y$的偏导数。
$\dfrac {\partial f}{\partial x}=\dfrac {\partial (6x-{x}^{2})(4y-{y}^{2})}{\partial x}=(4y-{y}^{2})(6-2x)$
$\dfrac {\partial f}{\partial y}=\dfrac {\partial (6x-{x}^{2})(4y-{y}^{2})}{\partial y}=(6x-{x}^{2})(4-2y)$
步骤 2:求驻点
令偏导数等于0,求出驻点。
$\left \{ \begin{matrix} (4y-{y}^{2})(6-2x)=0\\ (6x-{x}^{2})(4-2y)=0\end{matrix} \right.$
解得:
${x}_{1}=0$ ${y}_{1}=0$
${x}_{2}=0$ ${y}_{2}=4$
${x}_{3}=3$ ${y}_{3}=2$
${x}_{4}=6$ ${y}_{4}=0$
${x}_{5}=6$ ${y}_{5}=4$
步骤 3:求二阶偏导数
求出二阶偏导数,用于判断极值。
${x}_{xx}(x,y)=-2(4y-{y}^{2})$
${x}_{xy}(x,y)=4(3-x)(2-y)$
${y}_{yy}(x,y)=-2(6x-{x}^{2})$
步骤 4:判断极值
根据二阶偏导数的值,判断每个驻点是否为极值点。
在点(0,0)处,$A={f}_{xx}(0,0)=0$ $B={f}_{xy}(0,0)=24$ $C={f}_{yy}(0,0)=0$
$AC-{B}^{2}=-{24}^{2}\lt 0$,故f(0,0)不是极值。
在点(0,4)处,$A={f}_{xx}(0,4)=0$ $B={f}_{xy}(0,4)=-24$ $C={f}_{yy}(0,4)=0$
$AC-{B}^{2}=-{24}^{2}\lt 0$,故f(0,4)不是极值。
在点(3,2)处,$A={f}_{xx}(3,2)=-8$ $B={f}_{xy}(3,2)=0$ $C={f}_{yy}(3,2)=-18$
$AC-{B}^{2}=144\gt 0$,故在点f(3,2)处取得极大值。极大值f(3,2)=36
在点(6,0)处,$A={f}_{xx}(6,0)=0$ $B={f}_{xy}(6,0)=-24$ $C={f}_{yy}(6,0)=0$
$AC-{B}^{2}=-{24}^{2}\lt 0$,故f(6,0)不是极值。
在点(6,4)处,$A={f}_{xx}(6,4)=0$ $B={f}_{xy}(6,4)=24$ $C={f}_{yy}(6,4)=0$
$AC-{B}^{2}=-{24}^{2}\lt 0$,故f(6,4)不是极值。
首先,我们需要求出函数$f(x;y)=(6x-{x}^{2})(4y-{y}^{2})$关于$x$和$y$的偏导数。
$\dfrac {\partial f}{\partial x}=\dfrac {\partial (6x-{x}^{2})(4y-{y}^{2})}{\partial x}=(4y-{y}^{2})(6-2x)$
$\dfrac {\partial f}{\partial y}=\dfrac {\partial (6x-{x}^{2})(4y-{y}^{2})}{\partial y}=(6x-{x}^{2})(4-2y)$
步骤 2:求驻点
令偏导数等于0,求出驻点。
$\left \{ \begin{matrix} (4y-{y}^{2})(6-2x)=0\\ (6x-{x}^{2})(4-2y)=0\end{matrix} \right.$
解得:
${x}_{1}=0$ ${y}_{1}=0$
${x}_{2}=0$ ${y}_{2}=4$
${x}_{3}=3$ ${y}_{3}=2$
${x}_{4}=6$ ${y}_{4}=0$
${x}_{5}=6$ ${y}_{5}=4$
步骤 3:求二阶偏导数
求出二阶偏导数,用于判断极值。
${x}_{xx}(x,y)=-2(4y-{y}^{2})$
${x}_{xy}(x,y)=4(3-x)(2-y)$
${y}_{yy}(x,y)=-2(6x-{x}^{2})$
步骤 4:判断极值
根据二阶偏导数的值,判断每个驻点是否为极值点。
在点(0,0)处,$A={f}_{xx}(0,0)=0$ $B={f}_{xy}(0,0)=24$ $C={f}_{yy}(0,0)=0$
$AC-{B}^{2}=-{24}^{2}\lt 0$,故f(0,0)不是极值。
在点(0,4)处,$A={f}_{xx}(0,4)=0$ $B={f}_{xy}(0,4)=-24$ $C={f}_{yy}(0,4)=0$
$AC-{B}^{2}=-{24}^{2}\lt 0$,故f(0,4)不是极值。
在点(3,2)处,$A={f}_{xx}(3,2)=-8$ $B={f}_{xy}(3,2)=0$ $C={f}_{yy}(3,2)=-18$
$AC-{B}^{2}=144\gt 0$,故在点f(3,2)处取得极大值。极大值f(3,2)=36
在点(6,0)处,$A={f}_{xx}(6,0)=0$ $B={f}_{xy}(6,0)=-24$ $C={f}_{yy}(6,0)=0$
$AC-{B}^{2}=-{24}^{2}\lt 0$,故f(6,0)不是极值。
在点(6,4)处,$A={f}_{xx}(6,4)=0$ $B={f}_{xy}(6,4)=24$ $C={f}_{yy}(6,4)=0$
$AC-{B}^{2}=-{24}^{2}\lt 0$,故f(6,4)不是极值。