题目
将函数(x)=dfrac (1)(2-x)展开成x的幂级数,并求其收敛域。
将函数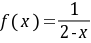
展开成x的幂级数,并求其收敛域。
题目解答
答案
解:由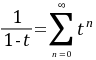
,-1<t<1
所以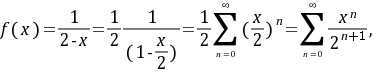
因为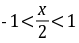
,所以-2<x<2
所以收敛域为(-2,2)
解析
步骤 1：将函数转换为幂级数形式
首先，我们注意到函数$f(x)=\dfrac {1}{2-x}$可以被重写为$f(x)=\dfrac {1}{2}\cdot \dfrac {1}{1-\dfrac {x}{2}}$。这一步是通过将分母中的2提取出来，使得剩余部分符合几何级数的通项形式$\dfrac {1}{1-r}$，其中$r=\dfrac {x}{2}$。
步骤 2：应用几何级数公式
几何级数的公式是$\sum _{n=0}^{\infty }{r}^{n}=\dfrac {1}{1-r}$，其中$|r|<1$。将$r=\dfrac {x}{2}$代入，我们得到$\dfrac {1}{1-\dfrac {x}{2}}=\sum _{n=0}^{\infty }{(\dfrac {x}{2})}^{n}$。因此，$f(x)=\dfrac {1}{2}\cdot \sum _{n=0}^{\infty }{(\dfrac {x}{2})}^{n}$。
步骤 3：确定幂级数的收敛域
幂级数$\sum _{n=0}^{\infty }{(\dfrac {x}{2})}^{n}$收敛的条件是$|\dfrac {x}{2}|<1$，即$-1<\dfrac {x}{2}<1$。解这个不等式，我们得到$-2
首先，我们注意到函数$f(x)=\dfrac {1}{2-x}$可以被重写为$f(x)=\dfrac {1}{2}\cdot \dfrac {1}{1-\dfrac {x}{2}}$。这一步是通过将分母中的2提取出来，使得剩余部分符合几何级数的通项形式$\dfrac {1}{1-r}$，其中$r=\dfrac {x}{2}$。
步骤 2：应用几何级数公式
几何级数的公式是$\sum _{n=0}^{\infty }{r}^{n}=\dfrac {1}{1-r}$，其中$|r|<1$。将$r=\dfrac {x}{2}$代入，我们得到$\dfrac {1}{1-\dfrac {x}{2}}=\sum _{n=0}^{\infty }{(\dfrac {x}{2})}^{n}$。因此，$f(x)=\dfrac {1}{2}\cdot \sum _{n=0}^{\infty }{(\dfrac {x}{2})}^{n}$。
步骤 3：确定幂级数的收敛域
幂级数$\sum _{n=0}^{\infty }{(\dfrac {x}{2})}^{n}$收敛的条件是$|\dfrac {x}{2}|<1$，即$-1<\dfrac {x}{2}<1$。解这个不等式，我们得到$-2