题目
--- 设随机变量X的概率密度为-|||-(1) f(x)= ) 2(1-1/(x)^2) 0, .-|||-求X的分布函数F (x),并画出(2)中的f(x)及F(x)的图形.

题目解答
答案
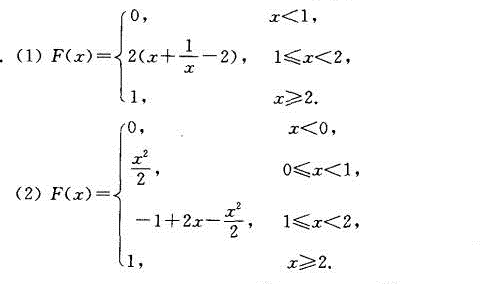
解析
步骤 1:计算分布函数F(x)的表达式
对于随机变量X的概率密度函数f(x),其分布函数F(x)定义为F(x) = P(X ≤ x) = ∫_{-∞}^{x} f(t) dt。根据题目中给出的f(x)的定义,我们需要分段计算F(x)的表达式。
步骤 2:计算(1)中的分布函数F(x)
对于(1)中的f(x),当x < 1时,f(x) = 0,因此F(x) = 0。当1 ≤ x ≤ 2时,F(x) = ∫_{1}^{x} 2(1 - 1/t^2) dt。当x > 2时,f(x) = 0,因此F(x) = 1。
步骤 3:计算(2)中的分布函数F(x)
对于(2)中的f(x),当x < 0时,f(x) = 0,因此F(x) = 0。当0 ≤ x < 1时,F(x) = ∫_{0}^{x} t dt。当1 ≤ x < 2时,F(x) = ∫_{0}^{1} t dt + ∫_{1}^{x} (2 - t) dt。当x ≥ 2时,f(x) = 0,因此F(x) = 1。
步骤 4:画出(2)中的f(x)及F(x)的图形
根据(2)中的f(x)和F(x)的表达式,可以画出它们的图形。f(x)在0 ≤ x < 1时为一条斜率为1的直线,在1 ≤ x < 2时为一条斜率为-1的直线。F(x)在0 ≤ x < 1时为一条斜率为1/2的直线,在1 ≤ x < 2时为一条斜率为1/2的抛物线。
对于随机变量X的概率密度函数f(x),其分布函数F(x)定义为F(x) = P(X ≤ x) = ∫_{-∞}^{x} f(t) dt。根据题目中给出的f(x)的定义,我们需要分段计算F(x)的表达式。
步骤 2:计算(1)中的分布函数F(x)
对于(1)中的f(x),当x < 1时,f(x) = 0,因此F(x) = 0。当1 ≤ x ≤ 2时,F(x) = ∫_{1}^{x} 2(1 - 1/t^2) dt。当x > 2时,f(x) = 0,因此F(x) = 1。
步骤 3:计算(2)中的分布函数F(x)
对于(2)中的f(x),当x < 0时,f(x) = 0,因此F(x) = 0。当0 ≤ x < 1时,F(x) = ∫_{0}^{x} t dt。当1 ≤ x < 2时,F(x) = ∫_{0}^{1} t dt + ∫_{1}^{x} (2 - t) dt。当x ≥ 2时,f(x) = 0,因此F(x) = 1。
步骤 4:画出(2)中的f(x)及F(x)的图形
根据(2)中的f(x)和F(x)的表达式,可以画出它们的图形。f(x)在0 ≤ x < 1时为一条斜率为1的直线,在1 ≤ x < 2时为一条斜率为-1的直线。F(x)在0 ≤ x < 1时为一条斜率为1/2的直线,在1 ≤ x < 2时为一条斜率为1/2的抛物线。