题目
计算下列定积分:(int )_(-1)^1dfrac (x)(sqrt {5-4x)}dx;
计算下列定积分:
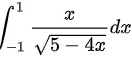 ;
;
题目解答
答案
设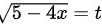
即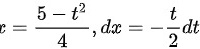
换积分上下限:当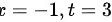 ;当
;当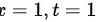
∴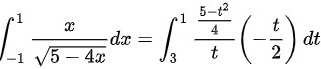
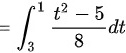
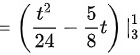
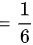
解析
步骤 1:换元
设$\sqrt {5-4x}=t$,则$x=\dfrac {5-{t}^{2}}{4}$,$dx=-\dfrac {t}{2}dt$。
步骤 2:确定积分上下限
当$x=-1$时,$t=3$;当$x=1$时,$t=1$。
步骤 3:代入换元后的积分
${\int }_{-1}^{1}\dfrac {x}{\sqrt {5-4x}}dx={\int }_{3}^{1}\dfrac {\dfrac {5-{t}^{2}}{4}}{t}(-\dfrac {t}{2})dt$。
步骤 4:化简积分
${\int }_{3}^{1}\dfrac {\dfrac {5-{t}^{2}}{4}}{t}(-\dfrac {t}{2})dt={\int }_{3}^{1}\dfrac {{t}^{2}-5}{8}dt$。
步骤 5:计算积分
${\int }_{3}^{1}\dfrac {{t}^{2}-5}{8}dt=(\dfrac {{t}^{3}}{24}-\dfrac {5}{8}t)|_{3}^{1}$。
步骤 6:代入上下限
$(\dfrac {{t}^{3}}{24}-\dfrac {5}{8}t)|_{3}^{1}=(\dfrac {1}{24}-\dfrac {5}{8})-(\dfrac {27}{24}-\dfrac {15}{8})$。
步骤 7:计算结果
$(\dfrac {1}{24}-\dfrac {5}{8})-(\dfrac {27}{24}-\dfrac {15}{8})=\dfrac {1}{6}$。
设$\sqrt {5-4x}=t$,则$x=\dfrac {5-{t}^{2}}{4}$,$dx=-\dfrac {t}{2}dt$。
步骤 2:确定积分上下限
当$x=-1$时,$t=3$;当$x=1$时,$t=1$。
步骤 3:代入换元后的积分
${\int }_{-1}^{1}\dfrac {x}{\sqrt {5-4x}}dx={\int }_{3}^{1}\dfrac {\dfrac {5-{t}^{2}}{4}}{t}(-\dfrac {t}{2})dt$。
步骤 4:化简积分
${\int }_{3}^{1}\dfrac {\dfrac {5-{t}^{2}}{4}}{t}(-\dfrac {t}{2})dt={\int }_{3}^{1}\dfrac {{t}^{2}-5}{8}dt$。
步骤 5:计算积分
${\int }_{3}^{1}\dfrac {{t}^{2}-5}{8}dt=(\dfrac {{t}^{3}}{24}-\dfrac {5}{8}t)|_{3}^{1}$。
步骤 6:代入上下限
$(\dfrac {{t}^{3}}{24}-\dfrac {5}{8}t)|_{3}^{1}=(\dfrac {1}{24}-\dfrac {5}{8})-(\dfrac {27}{24}-\dfrac {15}{8})$。
步骤 7:计算结果
$(\dfrac {1}{24}-\dfrac {5}{8})-(\dfrac {27}{24}-\dfrac {15}{8})=\dfrac {1}{6}$。