题目
[5.1]设离散型随机变量X的分布律为: X=k =b(lambda )^k , (k=1,2,3,... ) 且 gt 0,-|||-则λ为 ()-|||-(A) lambda gt 0 的任意实数 (B) lambda =b+1 (C) lambda =dfrac (1)(1+b) (D) lambda =dfrac (1)(b-1)

题目解答
答案
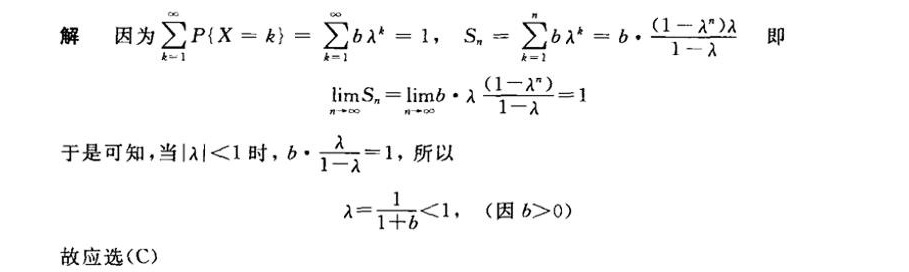
解析
考查要点:本题主要考查离散型随机变量分布律的性质,即所有可能取值的概率之和为1,以及等比数列求和公式的应用。
解题核心思路:
- 分布律归一性:根据概率分布的性质,所有概率之和必须等于1,即$\sum_{k=1}^{\infty} P\{X=k\} = 1$。
- 等比数列求和:将题目中的概率表达式转化为等比数列求和形式,利用公比$|\lambda| < 1$的条件求和。
- 解方程求$\lambda$:通过等比数列和为1的方程,解出$\lambda$的表达式,并验证其合理性。
破题关键点:
- 识别等比数列结构:概率表达式$b\lambda^k$是首项为$b\lambda$、公比为$\lambda$的等比数列。
- 收敛条件:公比$|\lambda| < 1$是级数收敛的前提,结合$b > 0$进一步限定$\lambda$的范围。
根据分布律的归一性条件,所有概率之和为1:
$\sum_{k=1}^{\infty} P\{X=k\} = \sum_{k=1}^{\infty} b\lambda^k = 1.$
步骤1:等比数列求和
该级数是首项为$b\lambda$、公比为$\lambda$的等比数列。当$|\lambda| < 1$时,其和为:
$\sum_{k=1}^{\infty} b\lambda^k = b\lambda \cdot \frac{1}{1 - \lambda} = \frac{b\lambda}{1 - \lambda}.$
步骤2:建立方程并求解
根据归一性条件,令和等于1:
$\frac{b\lambda}{1 - \lambda} = 1.$
解方程:
- 两边同乘$(1 - \lambda)$:
$b\lambda = 1 - \lambda.$ - 移项整理:
$b\lambda + \lambda = 1 \quad \Rightarrow \quad \lambda(b + 1) = 1.$ - 解得:
$\lambda = \frac{1}{b + 1}.$
步骤3:验证合理性
- 由于$b > 0$,分母$b + 1 > 1$,因此$\lambda = \frac{1}{b + 1} < 1$,满足收敛条件。
- $\lambda > 0$(概率非负),符合题意。