题目
lim _(xarrow 0)((dfrac {1+tan x)(1+sin x))}^dfrac (1{-{x)^3}}.
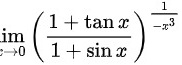 .
.
题目解答
答案
对于极限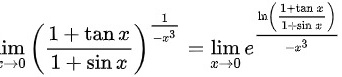 ,由等价无穷小可知,当
,由等价无穷小可知,当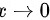 时,有
时,有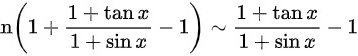 ,
,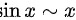 ,
,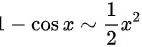 ,则极限
,则极限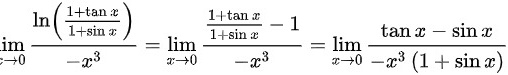
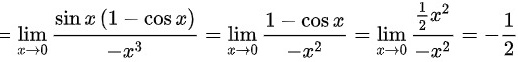 ,故极限
,故极限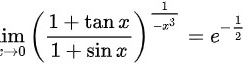 .
.
故答案为: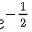
解析
步骤 1:将极限问题转化为指数形式
将原极限问题转化为指数形式,即$\lim _{x\rightarrow 0}{(\dfrac {1+\tan x}{1+\sin x})}^{\dfrac {1}{-{x}^{3}}}=\lim _{x\rightarrow 0}{e}^{\dfrac {\ln (\dfrac {1+\tan x}{1+\sin x})}{-{x}^{3}}}$。
步骤 2:利用等价无穷小替换
当$x\rightarrow 0$时,有$\ln(1+\dfrac {1+\tan x}{1+\sin x}-1)\sim \dfrac {1+\tan x}{1+\sin x}-1$,$\ln x\sim x$,$1-\cos x\sim \dfrac {1}{2}{x}^{2}$。因此,$\lim _{x\rightarrow 0}\dfrac {\ln (\dfrac {1+\tan x}{1+\sin x})}{-{x}^{3}}=\lim _{x\rightarrow 0}\dfrac {\dfrac {1+\tan x}{1+\sin x}-1}{-{x}^{3}}$。
步骤 3:化简并求极限
化简得到$\lim _{x\rightarrow 0}\dfrac {\tan x-\sin x}{-{x}^{3}(1+\sin x)}$,进一步化简为$\lim _{x\rightarrow 0}\dfrac {\sin x(1-\cos x)}{-{x}^{3}}$,再化简为$\lim _{x\rightarrow 0}\dfrac {1-\cos x}{-{x}^{2}}$,最后化简为$\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{2}{x}^{2}}{-{x}^{2}}=-\dfrac {1}{2}$。
步骤 4:求解原极限
根据步骤3的结果,原极限$\lim _{x\rightarrow 0}{(\dfrac {1+\tan x}{1+\sin x})}^{\dfrac {1}{-{x}^{3}}}={e}^{-\dfrac {1}{2}}$。
将原极限问题转化为指数形式,即$\lim _{x\rightarrow 0}{(\dfrac {1+\tan x}{1+\sin x})}^{\dfrac {1}{-{x}^{3}}}=\lim _{x\rightarrow 0}{e}^{\dfrac {\ln (\dfrac {1+\tan x}{1+\sin x})}{-{x}^{3}}}$。
步骤 2:利用等价无穷小替换
当$x\rightarrow 0$时,有$\ln(1+\dfrac {1+\tan x}{1+\sin x}-1)\sim \dfrac {1+\tan x}{1+\sin x}-1$,$\ln x\sim x$,$1-\cos x\sim \dfrac {1}{2}{x}^{2}$。因此,$\lim _{x\rightarrow 0}\dfrac {\ln (\dfrac {1+\tan x}{1+\sin x})}{-{x}^{3}}=\lim _{x\rightarrow 0}\dfrac {\dfrac {1+\tan x}{1+\sin x}-1}{-{x}^{3}}$。
步骤 3:化简并求极限
化简得到$\lim _{x\rightarrow 0}\dfrac {\tan x-\sin x}{-{x}^{3}(1+\sin x)}$,进一步化简为$\lim _{x\rightarrow 0}\dfrac {\sin x(1-\cos x)}{-{x}^{3}}$,再化简为$\lim _{x\rightarrow 0}\dfrac {1-\cos x}{-{x}^{2}}$,最后化简为$\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{2}{x}^{2}}{-{x}^{2}}=-\dfrac {1}{2}$。
步骤 4:求解原极限
根据步骤3的结果,原极限$\lim _{x\rightarrow 0}{(\dfrac {1+\tan x}{1+\sin x})}^{\dfrac {1}{-{x}^{3}}}={e}^{-\dfrac {1}{2}}$。