题目
18.设 = (x,y)|0leqslant yleqslant sqrt {4-{x)^2}} , 计算二重积分-|||-iint ((x)^2+(y)^2+xsin (y)^2)dxdy.
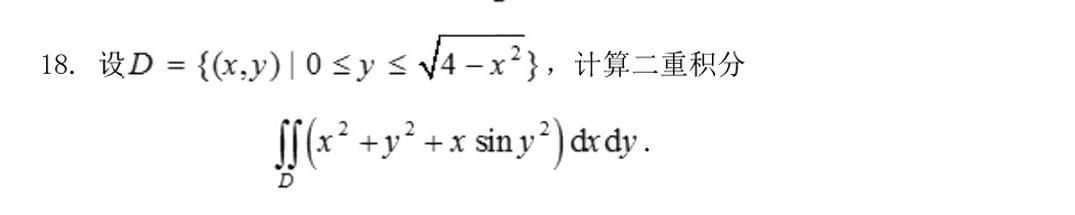
题目解答
答案

解析
步骤 1:确定积分区域
$D=\{ (x,y)|0\leqslant y\leqslant \sqrt {4-{x}^{2}}\} $,表示一个半径为2的上半圆区域,其中$-2\leqslant x\leqslant 2$,$0\leqslant y\leqslant 2$。
步骤 2:计算二重积分
$\iint ({x}^{2}+{y}^{2}+x\sin {y}^{2})dxdy$,首先对$x$积分,然后对$y$积分。
步骤 3:对$x$积分
${\int }_{-2}^{2}({x}^{2}+{y}^{2}+x\sin {y}^{2})dx$,计算得到$\dfrac {1}{3}{x}^{3}+{y}^{2}x+x\sin {y}^{2}$在$-2$到$2$的积分值。
步骤 4:对$y$积分
将步骤3的结果代入,得到${\int }_{0}^{2}(\dfrac {16}{3}+4{y}^{2}+4\sin {y}^{2})dy$,计算得到$\dfrac {32}{3}+\dfrac {32}{3}+2(y-\dfrac {1}{2}\sin 2y)$在$0$到$2$的积分值。
步骤 5:计算最终结果
将步骤4的结果代入,得到$\dfrac {64}{3}+4-\sin 4$。
$D=\{ (x,y)|0\leqslant y\leqslant \sqrt {4-{x}^{2}}\} $,表示一个半径为2的上半圆区域,其中$-2\leqslant x\leqslant 2$,$0\leqslant y\leqslant 2$。
步骤 2:计算二重积分
$\iint ({x}^{2}+{y}^{2}+x\sin {y}^{2})dxdy$,首先对$x$积分,然后对$y$积分。
步骤 3:对$x$积分
${\int }_{-2}^{2}({x}^{2}+{y}^{2}+x\sin {y}^{2})dx$,计算得到$\dfrac {1}{3}{x}^{3}+{y}^{2}x+x\sin {y}^{2}$在$-2$到$2$的积分值。
步骤 4:对$y$积分
将步骤3的结果代入,得到${\int }_{0}^{2}(\dfrac {16}{3}+4{y}^{2}+4\sin {y}^{2})dy$,计算得到$\dfrac {32}{3}+\dfrac {32}{3}+2(y-\dfrac {1}{2}\sin 2y)$在$0$到$2$的积分值。
步骤 5:计算最终结果
将步骤4的结果代入,得到$\dfrac {64}{3}+4-\sin 4$。