题目
6.设线性方程组 ) (x)_(1)-(x)_(2)-(x)_(3)=1 (x)_(1)+lambda (x)_(2)+(x)_(3)=1 -(x)_(1)+(x)_(2)+lambda (x)_(3)=1 . 有唯一解,则λ的值-|||-应为 () .-|||-(A)0; (B)1;-|||-(C) -1 ; (D)异于0与 pm 1 的实数.
题目解答
答案
解析
步骤 1:写出线性方程组的系数矩阵和增广矩阵
线性方程组的系数矩阵为:
$$
A = \begin{pmatrix}
\lambda & -1 & -1 \\
1 & \lambda & 1 \\
-1 & 1 & \lambda
\end{pmatrix}
$$
增广矩阵为:
$$
\begin{pmatrix}
\lambda & -1 & -1 & 1 \\
1 & \lambda & 1 & 1 \\
-1 & 1 & \lambda & 1
\end{pmatrix}
$$
步骤 2:计算系数矩阵的行列式
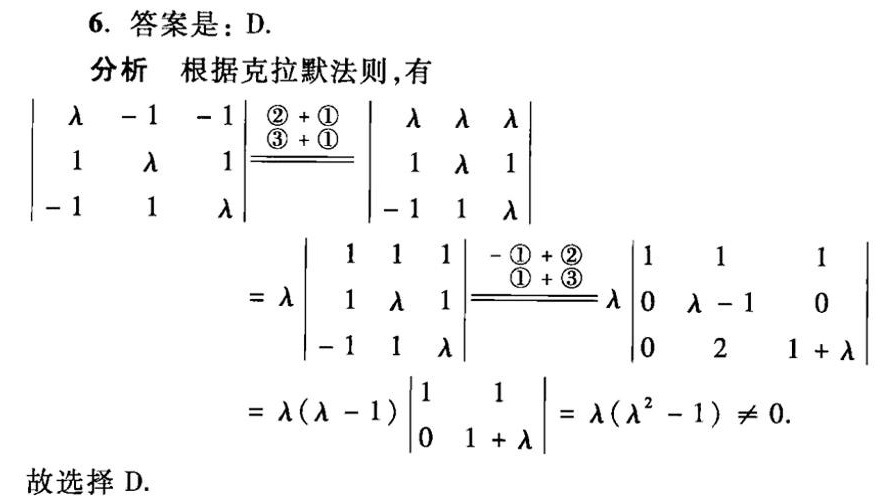
根据克拉默法则,线性方程组有唯一解的条件是系数矩阵的行列式不为零。计算行列式:
$$
\det(A) = \begin{vmatrix}
\lambda & -1 & -1 \\
1 & \lambda & 1 \\
-1 & 1 & \lambda
\end{vmatrix}
$$
步骤 3:展开行列式
$$
\det(A) = \lambda \begin{vmatrix}
\lambda & 1 \\
1 & \lambda
\end{vmatrix} - (-1) \begin{vmatrix}
1 & 1 \\
-1 & \lambda
\end{vmatrix} + (-1) \begin{vmatrix}
1 & \lambda \\
-1 & 1
\end{vmatrix}
$$
$$
= \lambda(\lambda^2 - 1) + (1 + \lambda) - (\lambda + 1)
$$
$$
= \lambda^3 - \lambda + 1 + \lambda - \lambda - 1
$$
$$
= \lambda^3 - \lambda
$$
$$
= \lambda(\lambda^2 - 1)
$$
$$
= \lambda(\lambda - 1)(\lambda + 1)
$$
步骤 4:确定行列式不为零的条件
为了使线性方程组有唯一解,行列式 $\det(A)$ 必须不为零,即:
$$
\lambda(\lambda - 1)(\lambda + 1) \neq 0
$$
这意味着 $\lambda$ 不能取 $0$、$1$ 或 $-1$。
线性方程组的系数矩阵为:
$$
A = \begin{pmatrix}
\lambda & -1 & -1 \\
1 & \lambda & 1 \\
-1 & 1 & \lambda
\end{pmatrix}
$$
增广矩阵为:
$$
\begin{pmatrix}
\lambda & -1 & -1 & 1 \\
1 & \lambda & 1 & 1 \\
-1 & 1 & \lambda & 1
\end{pmatrix}
$$
步骤 2:计算系数矩阵的行列式
根据克拉默法则,线性方程组有唯一解的条件是系数矩阵的行列式不为零。计算行列式:
$$
\det(A) = \begin{vmatrix}
\lambda & -1 & -1 \\
1 & \lambda & 1 \\
-1 & 1 & \lambda
\end{vmatrix}
$$
步骤 3:展开行列式
$$
\det(A) = \lambda \begin{vmatrix}
\lambda & 1 \\
1 & \lambda
\end{vmatrix} - (-1) \begin{vmatrix}
1 & 1 \\
-1 & \lambda
\end{vmatrix} + (-1) \begin{vmatrix}
1 & \lambda \\
-1 & 1
\end{vmatrix}
$$
$$
= \lambda(\lambda^2 - 1) + (1 + \lambda) - (\lambda + 1)
$$
$$
= \lambda^3 - \lambda + 1 + \lambda - \lambda - 1
$$
$$
= \lambda^3 - \lambda
$$
$$
= \lambda(\lambda^2 - 1)
$$
$$
= \lambda(\lambda - 1)(\lambda + 1)
$$
步骤 4:确定行列式不为零的条件
为了使线性方程组有唯一解,行列式 $\det(A)$ 必须不为零,即:
$$
\lambda(\lambda - 1)(\lambda + 1) \neq 0
$$
这意味着 $\lambda$ 不能取 $0$、$1$ 或 $-1$。