题目
画出积分区域，并计算下列二重积分：iint ((x)^2+(y)^2-x)dsigma ，其中D是由直线iint ((x)^2+(y)^2-x)dsigma 及iint ((x)^2+(y)^2-x)dsigma 所围成的闭区域
画出积分区域，并计算下列二重积分：
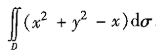，其中D是由直线
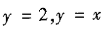及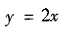
所围成的闭区域
题目解答
答案
解析
步骤 1：确定积分区域
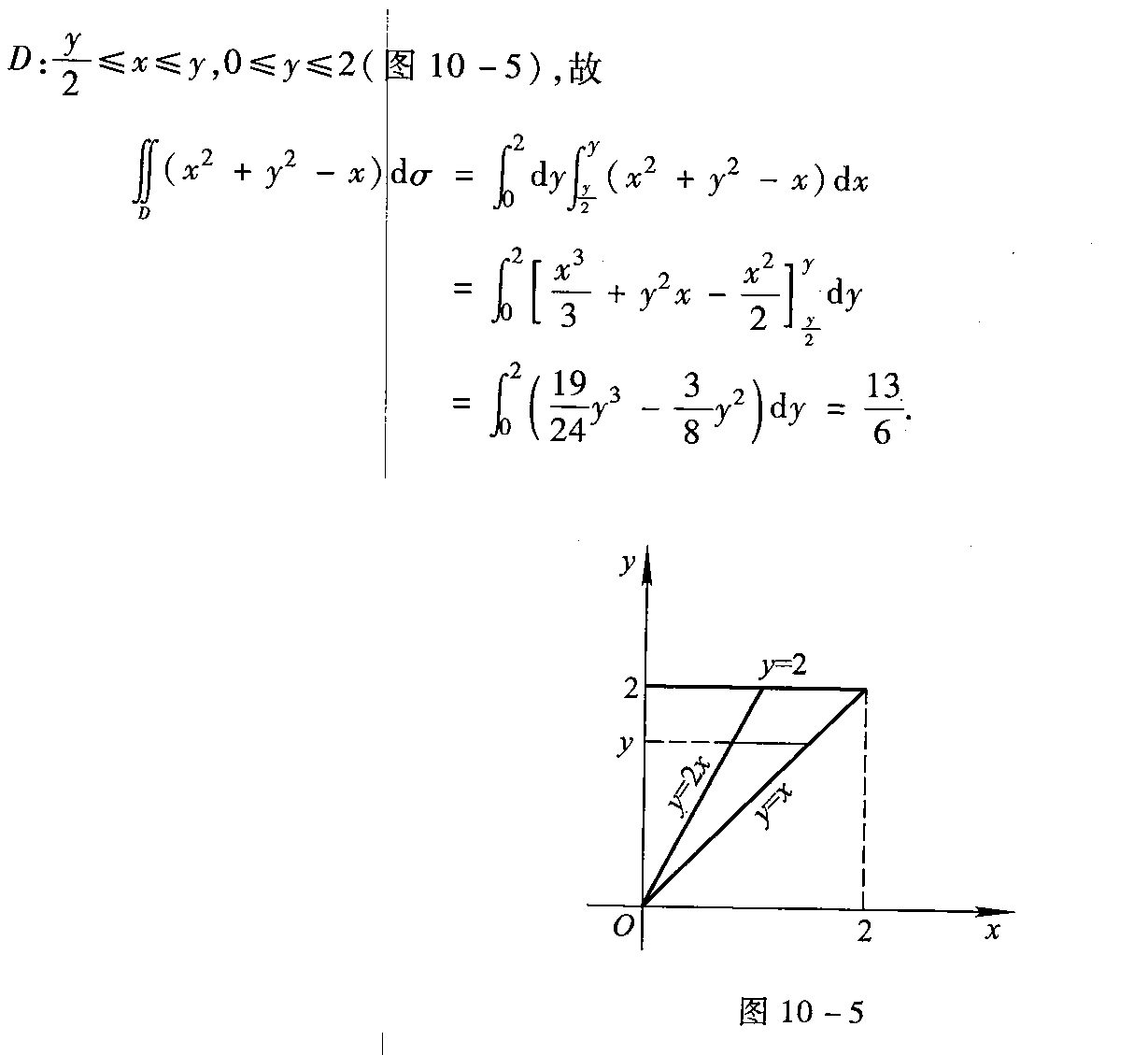
根据题目，积分区域D是由直线y=2，y=x及y=2x所围成的闭区域。首先，我们需要画出这些直线，确定它们的交点，从而确定积分区域D的边界。
步骤 2：确定积分区域的边界
直线y=2与y=x的交点为(2,2)，直线y=2与y=2x的交点为(1,2)，直线y=x与y=2x的交点为(0,0)。因此，积分区域D的边界为y=2，x=y/2，x=y。
步骤 3：计算二重积分
根据积分区域D的边界，我们可以将二重积分表示为：
$\iint ({x}^{2}+{y}^{2}-x)d\sigma ={\int }_{0}^{2}dy{\int }_{\dfrac {y}{2}}^{y}({x}^{2}+{y}^{2}-x)dx$
步骤 4：计算内层积分
计算内层积分，即对x进行积分：
${\int }_{\dfrac {y}{2}}^{y}({x}^{2}+{y}^{2}-x)dx = [\dfrac {x^3}{3} + y^2x - \dfrac {x^2}{2}]_{\dfrac {y}{2}}^{y}$
步骤 5：计算外层积分
计算外层积分，即对y进行积分：
${\int }_{0}^{2}[\dfrac {x^3}{3} + y^2x - \dfrac {x^2}{2}]_{\dfrac {y}{2}}^{y}dy = {\int }_{0}^{2}(\dfrac {19}{24}y^3 - \dfrac {3}{8}y^2)dy$
步骤 6：计算最终结果
计算最终结果，即对y进行积分：
${\int }_{0}^{2}(\dfrac {19}{24}y^3 - \dfrac {3}{8}y^2)dy = \dfrac {13}{6}$
根据题目，积分区域D是由直线y=2，y=x及y=2x所围成的闭区域。首先，我们需要画出这些直线，确定它们的交点，从而确定积分区域D的边界。
步骤 2：确定积分区域的边界
直线y=2与y=x的交点为(2,2)，直线y=2与y=2x的交点为(1,2)，直线y=x与y=2x的交点为(0,0)。因此，积分区域D的边界为y=2，x=y/2，x=y。
步骤 3：计算二重积分
根据积分区域D的边界，我们可以将二重积分表示为：
$\iint ({x}^{2}+{y}^{2}-x)d\sigma ={\int }_{0}^{2}dy{\int }_{\dfrac {y}{2}}^{y}({x}^{2}+{y}^{2}-x)dx$
步骤 4：计算内层积分
计算内层积分，即对x进行积分：
${\int }_{\dfrac {y}{2}}^{y}({x}^{2}+{y}^{2}-x)dx = [\dfrac {x^3}{3} + y^2x - \dfrac {x^2}{2}]_{\dfrac {y}{2}}^{y}$
步骤 5：计算外层积分
计算外层积分，即对y进行积分：
${\int }_{0}^{2}[\dfrac {x^3}{3} + y^2x - \dfrac {x^2}{2}]_{\dfrac {y}{2}}^{y}dy = {\int }_{0}^{2}(\dfrac {19}{24}y^3 - \dfrac {3}{8}y^2)dy$
步骤 6：计算最终结果
计算最终结果，即对y进行积分：
${\int }_{0}^{2}(\dfrac {19}{24}y^3 - \dfrac {3}{8}y^2)dy = \dfrac {13}{6}$