题目
4.设∑表示圆柱面 ^2+(y)^2=(R)^2 介于 z=0 和 z=2 之间的部分,则曲面积分-|||-int (dfrac (1)(sqrt {{x)^2+(y)^2}}-y)ds= 【 】-|||-(A) 2pi R (B) 2π (C)4pi R (D)4pi
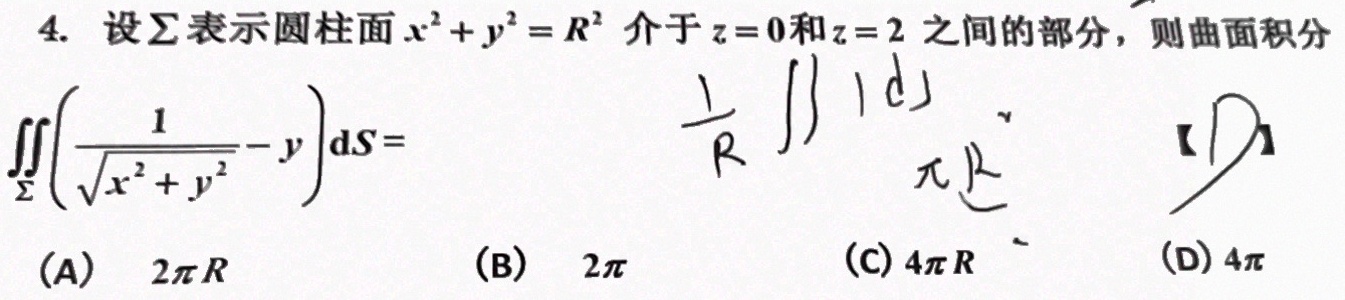
题目解答
答案

解析
步骤 1:确定曲面的参数化
圆柱面 ${x}^{2}+{y}^{2}={R}^{2}$ 可以用参数方程表示为 $x=R\cos\theta$,$y=R\sin\theta$,$z=z$,其中 $0\leq\theta\leq2\pi$,$0\leq z\leq2$。
步骤 2:计算曲面元素 $dS$
曲面元素 $dS$ 可以表示为 $dS=Rd\theta dz$,因为圆柱面的侧面积元素在 $z$ 方向上是 $dz$,在圆周方向上是 $Rd\theta$。
步骤 3:计算曲面积分
曲面积分可以表示为:
$$
\int_{\sum} \left(\frac{1}{\sqrt{x^2+y^2}}-y\right)dS = \int_{0}^{2\pi} \int_{0}^{2} \left(\frac{1}{R}-R\sin\theta\right)Rd\theta dz
$$
将积分分解为两个部分:
$$
\int_{0}^{2\pi} \int_{0}^{2} \frac{1}{R}Rd\theta dz - \int_{0}^{2\pi} \int_{0}^{2} R\sin\theta Rd\theta dz
$$
计算第一个积分:
$$
\int_{0}^{2\pi} \int_{0}^{2} d\theta dz = 2\pi \times 2 = 4\pi
$$
计算第二个积分:
$$
\int_{0}^{2\pi} \int_{0}^{2} R^2\sin\theta d\theta dz = R^2 \int_{0}^{2\pi} \sin\theta d\theta \int_{0}^{2} dz = R^2 \times 0 \times 2 = 0
$$
因此,曲面积分的结果为 $4\pi$。
圆柱面 ${x}^{2}+{y}^{2}={R}^{2}$ 可以用参数方程表示为 $x=R\cos\theta$,$y=R\sin\theta$,$z=z$,其中 $0\leq\theta\leq2\pi$,$0\leq z\leq2$。
步骤 2:计算曲面元素 $dS$
曲面元素 $dS$ 可以表示为 $dS=Rd\theta dz$,因为圆柱面的侧面积元素在 $z$ 方向上是 $dz$,在圆周方向上是 $Rd\theta$。
步骤 3:计算曲面积分
曲面积分可以表示为:
$$
\int_{\sum} \left(\frac{1}{\sqrt{x^2+y^2}}-y\right)dS = \int_{0}^{2\pi} \int_{0}^{2} \left(\frac{1}{R}-R\sin\theta\right)Rd\theta dz
$$
将积分分解为两个部分:
$$
\int_{0}^{2\pi} \int_{0}^{2} \frac{1}{R}Rd\theta dz - \int_{0}^{2\pi} \int_{0}^{2} R\sin\theta Rd\theta dz
$$
计算第一个积分:
$$
\int_{0}^{2\pi} \int_{0}^{2} d\theta dz = 2\pi \times 2 = 4\pi
$$
计算第二个积分:
$$
\int_{0}^{2\pi} \int_{0}^{2} R^2\sin\theta d\theta dz = R^2 \int_{0}^{2\pi} \sin\theta d\theta \int_{0}^{2} dz = R^2 \times 0 \times 2 = 0
$$
因此,曲面积分的结果为 $4\pi$。