题目
当arrow (x)_(0)时,arrow (x)_(0)的极限为A.1B.-1C.0D.不存在
当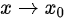 时,
时,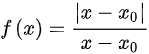 的极限为
的极限为
A.1
B.-1
C.0
D.不存在
题目解答
答案
D.不存在
当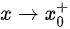 时,
时,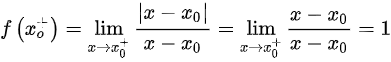
当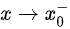 时,
时,
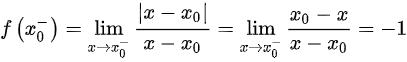
因为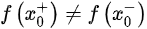
所以极限不存在。
解析
步骤 1:分析函数$f(x)=\dfrac {|x-{x}_{0}|}{x-{x}_{0}}$在$x\rightarrow {x}_{0}$时的左右极限。
当$x\rightarrow {{x}_{0}}^{+}$时,即$x$从右侧接近${x}_{0}$,此时$x-{x}_{0}$为正,$|x-{x}_{0}|=x-{x}_{0}$,因此$f(x)=\dfrac {|x-{x}_{0}|}{x-{x}_{0}}=\dfrac {x-{x}_{0}}{x-{x}_{0}}=1$。
步骤 2:分析函数$f(x)=\dfrac {|x-{x}_{0}|}{x-{x}_{0}}$在$x\rightarrow {x}_{0}$时的左极限。
当$x\rightarrow {{x}_{0}}^{-}$时,即$x$从左侧接近${x}_{0}$,此时$x-{x}_{0}$为负,$|x-{x}_{0}|={x}_{0}-x$,因此$f(x)=\dfrac {|x-{x}_{0}|}{x-{x}_{0}}=\dfrac {{x}_{0}-x}{x-{x}_{0}}=-1$。
步骤 3:判断极限是否存在。
由于$f({{x}_{0}}^{+})=1$和$f({{x}_{0}}^{-})=-1$,左右极限不相等,因此$f(x)=\dfrac {|x-{x}_{0}|}{x-{x}_{0}}$在$x\rightarrow {x}_{0}$时的极限不存在。
当$x\rightarrow {{x}_{0}}^{+}$时,即$x$从右侧接近${x}_{0}$,此时$x-{x}_{0}$为正,$|x-{x}_{0}|=x-{x}_{0}$,因此$f(x)=\dfrac {|x-{x}_{0}|}{x-{x}_{0}}=\dfrac {x-{x}_{0}}{x-{x}_{0}}=1$。
步骤 2:分析函数$f(x)=\dfrac {|x-{x}_{0}|}{x-{x}_{0}}$在$x\rightarrow {x}_{0}$时的左极限。
当$x\rightarrow {{x}_{0}}^{-}$时,即$x$从左侧接近${x}_{0}$,此时$x-{x}_{0}$为负,$|x-{x}_{0}|={x}_{0}-x$,因此$f(x)=\dfrac {|x-{x}_{0}|}{x-{x}_{0}}=\dfrac {{x}_{0}-x}{x-{x}_{0}}=-1$。
步骤 3:判断极限是否存在。
由于$f({{x}_{0}}^{+})=1$和$f({{x}_{0}}^{-})=-1$,左右极限不相等,因此$f(x)=\dfrac {|x-{x}_{0}|}{x-{x}_{0}}$在$x\rightarrow {x}_{0}$时的极限不存在。