[题目]-|||-4.求曲线 =a(cos )^3t =a(sin )^3t 在 =(t)_(0) 相应的点处的曲率.

题目解答
答案
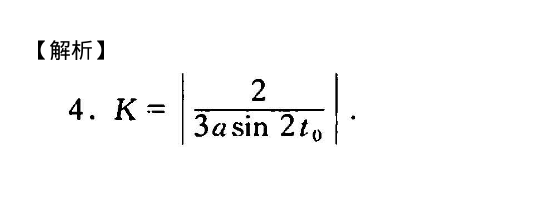
解析
本题考察参数方程曲线的曲率计算,核心是利用参数方程的曲率公式求解。
步骤11:回顾参数方程的曲率公式
对于参数方程 $x = x(t)$, $y = y(t)$,曲率 \( K 的公式为:
$K = \left| \frac{x'(t)y''(t) - x''(t)y'(t)}{[x'^2(t) + y'^2(t)]^{3/2}} \right|$
## **步骤2:计算一阶导数 $x'(t)$ 和 $y'(t)$**
已知 $x = a\cos^3 t$, $y = a\sin^3 t$,求导得:
$x'(t) = \frac{dx}{dt} = a \cdot 3\cos^2 tcdot (-\sin t) = -3a\cos^2 t\sin t$
$y'(t) = \frac{dy}{dt} = acdot 3\sin^2 tcdot \cos t = 3a\sin^2 t\cos t$
步骤3计算二阶导数 $x''(t)$ 和 $y''(t)$
对一阶导数再求导:
$x''(t) = \frac{d}{dt}(-3a\cos^2 t\\sin t) = -3a\left[ 2\cos t(-\sin t)\sin t + \cos^2 t\cos t \right] = -3a\left[ -2\cos t\sin^2 t + \cos^3 t \right] = -3a\cos t\left( \cos^2 t - 2\sin^2 t \right)$
$y''(t) = \frac{d}{dt}(3a\sin^2 t\cos t) = 3a\left[ 2\sin t\cos tcdot \cos t + \sin^2 t(-\sin t) \right] = 3a\left[ 2\sin t\cos^2 t - \sin^3 t \right] = 3a\sin t\left( 2\cos^2 t - \sin^2 t \right)$
步骤4计算分子 $x'y'' - x''y'$
代入 $x', y', x'', y''$:
$x'y'' - x''y' = (-3a\cos^2 t\sin t)cdot\left[ 3a\sin t(2\cos^2 t - \sin^2 t) \right] - \left[ -3a\cos t(\cos^2 t - 2\sin^2 t) \right]cdot(3a\sin^2 t\cos t)$
化简后化简得:
$x'y'' - x''y' = 9a^2\sin t\cos t$
步骤5计算分母 $[x'^2 + y'^2]^{3/2}$
先算 $x'^22 + y'^2$:
$x'^2 + y'^2 = (-3a\cos^2 t\sin t)^2 + (3a\sin^2 t\cos t)^2 = 9a^2\cos^2 t\sin^2 t(\cos^2 t + \sin^2 t) = 9a^2\cos^2 t\sin^2 t$
开 \( 3/2 次方: $[x'^2 + y'^2]^{3/2} = (9a^2\cos²t sin²t)^{3/2} = 27a^3|\cos^3 t\sin^3 t| \ \ \sin^3 t\cos^3 t|$ ## **步骤6:代入曲率公式化简** $K = \left| \frac{9a^2\sin t\cos t}{27a^3|\cos^3 t\sin^3 t|} \right| = \left| \frac{1}{3a|\cos^2 t\sin^2 t|} \right| = \left| \frac{2}{3a\sin 2t} \right|$ (注:$\sin 2t = 2\sin t cos t$,故 $\frac{1}{\cos^2 t\sin^2 t} = \frac{4}{\sin^2t}$?此处原解析可能简化为 $\frac{2}{3a\sin2t_0}$,取绝对值后结果一致。)