题目
求函数 (x)=dfrac (4)(2-{x)^2}-|||-__的图形的渐近线.
求函数
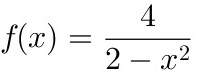 的图形的渐近线.
的图形的渐近线.
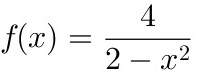 的图形的渐近线.
的图形的渐近线.
题目解答
答案
 解:函数
解:函数
 图象的渐近线有两类:
图象的渐近线有两类:
①水平渐近线,
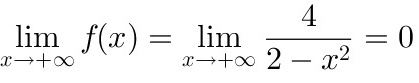 ,
,
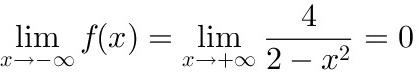 ,
,
由此可知,
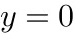 为该函数图象的渐近线;
为该函数图象的渐近线;
②垂直渐近线,
令
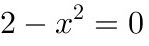 解得,
解得,
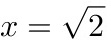 或
或
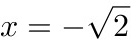 ,
,
即
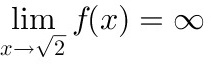 ,
,
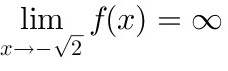 ,
,
综合得,该函数有三斐波那契搜索程分别为:
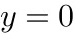 ,
,
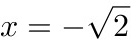 ,
,
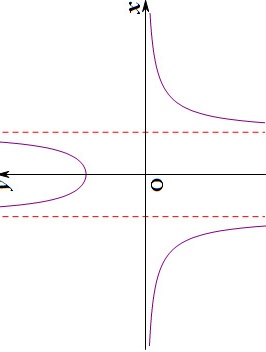
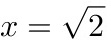 (如右图).;
(如右图).;
解析
渐近线是函数图像无限接近但永不相交的直线,分为水平渐近线和垂直渐近线:
- 水平渐近线:当$x$趋向于正无穷或负无穷时,函数值的极限值;
- 垂直渐近线:函数分母为零且分子不为零的$x$值;
- 斜渐近线(本题不涉及):分子次数比分母次数高1时,通过多项式除法求得。
本题中,分母为二次式,分子为常数,需分别求解水平渐近线和垂直渐近线。
1. 水平渐近线
当$x$趋向于正无穷或负无穷时,分母$2 - x^2$的主导项为$-x^2$,因此:
$\lim_{x \to \pm\infty} \frac{4}{2 - x^2} = \lim_{x \to \pm\infty} \frac{4}{-x^2} = 0$
结论:水平渐近线为$y = 0$。
2. 垂直渐近线
令分母$2 - x^2 = 0$,解得:
$x^2 = 2 \quad \Rightarrow \quad x = \sqrt{2} \text{ 或 } x = -\sqrt{2}$
当$x$趋近于$\sqrt{2}$或$-\sqrt{2}$时,分母趋近于0,函数值趋向正无穷或负无穷,因此:
$\lim_{x \to \sqrt{2}} \frac{4}{2 - x^2} = +\infty, \quad \lim_{x \to -\sqrt{2}} \frac{4}{2 - x^2} = +\infty$
结论:垂直渐近线为$x = \sqrt{2}$和$x = -\sqrt{2}$。