题目
计算 =11(x^2cosα+y^2cos β+z^2cosy)dS其中=11(x^2cosα+y^2cos β+z^2cosy)dS是曲面 =11(x^2cosα+y^2cos β+z^2cosy)dS介于=11(x^2cosα+y^2cos β+z^2cosy)dS与=11(x^2cosα+y^2cos β+z^2cosy)dS 之间的部分=11(x^2cosα+y^2cos β+z^2cosy)dS为 =11(x^2cosα+y^2cos β+z^2cosy)dS曲上任一 点 =11(x^2cosα+y^2cos β+z^2cosy)dS处指向外侧的法线向量的方向余弦
计算 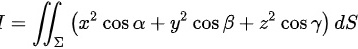 其中
其中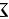 是曲面
是曲面 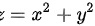 介于
介于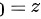 与
与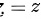 之间的部分
之间的部分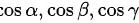 为
为 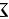 曲上任一 点
曲上任一 点 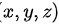 处指向外侧的法线向量的方向余弦
处指向外侧的法线向量的方向余弦
题目解答
答案
解:
平面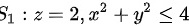 方向朝上,使
方向朝上,使
其与曲面S构成闭曲面
设它们所围成的区域为V,则由Gauss公式得
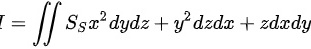
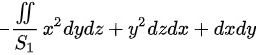
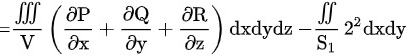
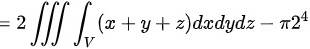

由于被积函数x、y分别是关于x和y的奇函数,而积分立体区域是关于yoz面和zox面对称的.
∴原式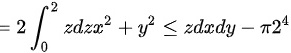
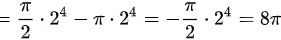
∴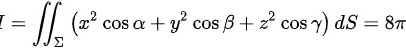
解析
步骤 1:确定曲面和积分区域
曲面 $S$ 由 $z = x^2 + y^2$ 给出,介于 $z = 1$ 和 $z = 4$ 之间。因此,积分区域 $D$ 在 $xy$ 平面上是一个半径从 $1$ 到 $2$ 的圆环。
步骤 2:应用高斯公式
考虑闭合曲面 $S$ 和平面 $S_1: z = 4$,它们共同围成一个闭合区域 $V$。根据高斯公式,有
$$
\iint_S (x^2 \cos \alpha + y^2 \cos \beta + z^2 \cos \gamma) dS = \iiint_V \left( \frac{\partial}{\partial x}(x^2) + \frac{\partial}{\partial y}(y^2) + \frac{\partial}{\partial z}(z^2) \right) dV - \iint_{S_1} (x^2 \cos \alpha + y^2 \cos \beta + z^2 \cos \gamma) dS.
$$
步骤 3:计算体积分
体积分 $\iiint_V (2x + 2y + 2z) dV$ 可以简化为 $\iiint_V 2z dV$,因为 $x$ 和 $y$ 的积分在对称区域中为零。因此,我们有
$$
\iiint_V 2z dV = 2 \iiint_V z dV.
$$
步骤 4:计算平面 $S_1$ 上的积分
平面 $S_1$ 上的积分 $\iint_{S_1} (x^2 \cos \alpha + y^2 \cos \beta + z^2 \cos \gamma) dS$ 可以简化为 $\iint_{S_1} z^2 dS$,因为 $z = 4$。因此,我们有
$$
\iint_{S_1} z^2 dS = \iint_{S_1} 4^2 dS = 16 \iint_{S_1} dS = 16 \pi \cdot 2^2 = 64 \pi.
$$
步骤 5:计算体积分 $\iiint_V z dV$
体积分 $\iiint_V z dV$ 可以通过柱坐标变换来计算。设 $x = r \cos \theta$,$y = r \sin \theta$,$z = z$,则有
$$
\iiint_V z dV = \int_0^{2\pi} \int_1^2 \int_{r^2}^4 z r dz dr d\theta = \int_0^{2\pi} \int_1^2 \left[ \frac{z^2}{2} \right]_{r^2}^4 r dr d\theta = \int_0^{2\pi} \int_1^2 \left( 8 - \frac{r^4}{2} \right) r dr d\theta = \int_0^{2\pi} \left[ 4r^2 - \frac{r^6}{12} \right]_1^2 d\theta = \int_0^{2\pi} \left( 16 - \frac{64}{12} - 4 + \frac{1}{12} \right) d\theta = \int_0^{2\pi} \left( 12 - \frac{63}{12} \right) d\theta = \int_0^{2\pi} \frac{69}{12} d\theta = \frac{69}{12} \cdot 2\pi = \frac{69\pi}{6} = \frac{23\pi}{2}.
$$
步骤 6:计算最终结果
将步骤 4 和步骤 5 的结果代入高斯公式,我们得到
$$
\iint_S (x^2 \cos \alpha + y^2 \cos \beta + z^2 \cos \gamma) dS = 2 \cdot \frac{23\pi}{2} - 64\pi = 23\pi - 64\pi = -41\pi.
$$
曲面 $S$ 由 $z = x^2 + y^2$ 给出,介于 $z = 1$ 和 $z = 4$ 之间。因此,积分区域 $D$ 在 $xy$ 平面上是一个半径从 $1$ 到 $2$ 的圆环。
步骤 2:应用高斯公式
考虑闭合曲面 $S$ 和平面 $S_1: z = 4$,它们共同围成一个闭合区域 $V$。根据高斯公式,有
$$
\iint_S (x^2 \cos \alpha + y^2 \cos \beta + z^2 \cos \gamma) dS = \iiint_V \left( \frac{\partial}{\partial x}(x^2) + \frac{\partial}{\partial y}(y^2) + \frac{\partial}{\partial z}(z^2) \right) dV - \iint_{S_1} (x^2 \cos \alpha + y^2 \cos \beta + z^2 \cos \gamma) dS.
$$
步骤 3:计算体积分
体积分 $\iiint_V (2x + 2y + 2z) dV$ 可以简化为 $\iiint_V 2z dV$,因为 $x$ 和 $y$ 的积分在对称区域中为零。因此,我们有
$$
\iiint_V 2z dV = 2 \iiint_V z dV.
$$
步骤 4:计算平面 $S_1$ 上的积分
平面 $S_1$ 上的积分 $\iint_{S_1} (x^2 \cos \alpha + y^2 \cos \beta + z^2 \cos \gamma) dS$ 可以简化为 $\iint_{S_1} z^2 dS$,因为 $z = 4$。因此,我们有
$$
\iint_{S_1} z^2 dS = \iint_{S_1} 4^2 dS = 16 \iint_{S_1} dS = 16 \pi \cdot 2^2 = 64 \pi.
$$
步骤 5:计算体积分 $\iiint_V z dV$
体积分 $\iiint_V z dV$ 可以通过柱坐标变换来计算。设 $x = r \cos \theta$,$y = r \sin \theta$,$z = z$,则有
$$
\iiint_V z dV = \int_0^{2\pi} \int_1^2 \int_{r^2}^4 z r dz dr d\theta = \int_0^{2\pi} \int_1^2 \left[ \frac{z^2}{2} \right]_{r^2}^4 r dr d\theta = \int_0^{2\pi} \int_1^2 \left( 8 - \frac{r^4}{2} \right) r dr d\theta = \int_0^{2\pi} \left[ 4r^2 - \frac{r^6}{12} \right]_1^2 d\theta = \int_0^{2\pi} \left( 16 - \frac{64}{12} - 4 + \frac{1}{12} \right) d\theta = \int_0^{2\pi} \left( 12 - \frac{63}{12} \right) d\theta = \int_0^{2\pi} \frac{69}{12} d\theta = \frac{69}{12} \cdot 2\pi = \frac{69\pi}{6} = \frac{23\pi}{2}.
$$
步骤 6:计算最终结果
将步骤 4 和步骤 5 的结果代入高斯公式,我们得到
$$
\iint_S (x^2 \cos \alpha + y^2 \cos \beta + z^2 \cos \gamma) dS = 2 \cdot \frac{23\pi}{2} - 64\pi = 23\pi - 64\pi = -41\pi.
$$