题目
https:/img.zuoyebang.cc/zyb_a148ede5fabdd95c53fd3b87a9e6b9b0.jpg+(a)_(1) 1 ... ... . 1-|||-1 https:/img.zuoyebang.cc/zyb_a148ede5fabdd95c53fd3b87a9e6b9b0.jpg+(a)_(2) ... ... . 1-|||-4.计算 _(n)=-|||-1 1 https:/img.zuoyebang.cc/zyb_a148ede5fabdd95c53fd3b87a9e6b9b0.jpg+(a)_(n)

题目解答
答案
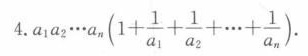
解析
步骤 1:行列式变换
首先,我们对行列式进行变换,以简化计算。我们可以通过行变换将行列式中的某些元素变为0,从而简化行列式的计算。具体地,我们可以将第1行减去第2行,第2行减去第3行,以此类推,直到第n-1行减去第n行。这样,我们就可以将行列式中的某些元素变为0,从而简化行列式的计算。
步骤 2:计算行列式
在进行行变换后,行列式变为:
$$
\left |\begin{matrix} {a}_{1}& -{a}_{2}& 0& 0\\ 0& {a}_{2}& -{a}_{3}& 0\\ 0& 0& {a}_{3}& -{a}_{4}\\ 0& 0& 0& {a}_{n}\end{matrix} | \right.
$$
这是一个上三角行列式,其值等于主对角线元素的乘积,即:
$$
{a}_{1}{a}_{2}\cdots {a}_{n}
$$
步骤 3:考虑最后一列
由于最后一列的元素为$1$,我们需要考虑最后一列对行列式值的影响。最后一列的元素为$1$,因此我们需要将最后一列的元素加到其他列中,以得到最终的行列式值。具体地,我们需要将最后一列的元素加到第1列、第2列、...、第n-1列中,以得到最终的行列式值。这样,我们就可以得到最终的行列式值为:
$$
{a}_{1}{a}_{2}\cdots {a}_{n}(1+\dfrac {1}{{a}_{1}}+\dfrac {1}{{a}_{2}}+\cdots +\dfrac {1}{{a}_{n}})
$$
首先,我们对行列式进行变换,以简化计算。我们可以通过行变换将行列式中的某些元素变为0,从而简化行列式的计算。具体地,我们可以将第1行减去第2行,第2行减去第3行,以此类推,直到第n-1行减去第n行。这样,我们就可以将行列式中的某些元素变为0,从而简化行列式的计算。
步骤 2:计算行列式
在进行行变换后,行列式变为:
$$
\left |\begin{matrix} {a}_{1}& -{a}_{2}& 0& 0\\ 0& {a}_{2}& -{a}_{3}& 0\\ 0& 0& {a}_{3}& -{a}_{4}\\ 0& 0& 0& {a}_{n}\end{matrix} | \right.
$$
这是一个上三角行列式,其值等于主对角线元素的乘积,即:
$$
{a}_{1}{a}_{2}\cdots {a}_{n}
$$
步骤 3:考虑最后一列
由于最后一列的元素为$1$,我们需要考虑最后一列对行列式值的影响。最后一列的元素为$1$,因此我们需要将最后一列的元素加到其他列中,以得到最终的行列式值。具体地,我们需要将最后一列的元素加到第1列、第2列、...、第n-1列中,以得到最终的行列式值。这样,我们就可以得到最终的行列式值为:
$$
{a}_{1}{a}_{2}\cdots {a}_{n}(1+\dfrac {1}{{a}_{1}}+\dfrac {1}{{a}_{2}}+\cdots +\dfrac {1}{{a}_{n}})
$$