题目
设函数y=f(x)在点取得极小值,则不正确的是A.'((x)_(0))=0A.'((x)_(0))=0A.'((x)_(0))=0A.'((x)_(0))=0
设函数y=f(x)在点取得极小值,则不正确的是
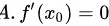
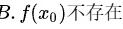
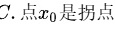
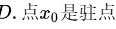
题目解答
答案
首先逐个分析每个选项,依据函数取得极小值的相关定理和概念来判断其正确性。
选项 A:如果函数y = f(x)在点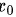 处可导并且取得极小值,根据极值存在的必要条件,导数
处可导并且取得极小值,根据极值存在的必要条件,导数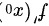 必然等于0。但如果函数在
必然等于0。但如果函数在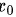 处不可导,也可能取得极小值,所以
处不可导,也可能取得极小值,所以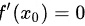 不是绝对的,只是一种可能情况。
不是绝对的,只是一种可能情况。
选项 B:当函数y = f(x)在点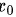 取得极小值时,
取得极小值时,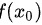 这个值是明确存在的,不能说
这个值是明确存在的,不能说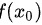 不存在,该选项说法错误。
不存在,该选项说法错误。
选项 C:极小值点和拐点是不同的概念。极小值点是函数值在该点附近局部最小的点;而拐点是函数凹凸性发生改变的点。一个点是极小值点并不意味着它一定是拐点,例如函数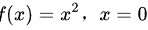 是极小值点,但不是拐点。
是极小值点,但不是拐点。
选项 D:如果函数在点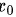 处可导并且取得极值,那么该点的导数
处可导并且取得极值,那么该点的导数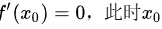 称为驻点。但如果函数在
称为驻点。但如果函数在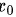 不可导,虽然取得极值,
不可导,虽然取得极值,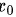 也不是驻点。所以说在可导的前提下,取得极小值的点是驻点,否则不一定。
也不是驻点。所以说在可导的前提下,取得极小值的点是驻点,否则不一定。
综上所述,不正确的是选项 B 和选项 C。
解析
考查要点:本题主要考查函数极值的定义、必要条件及相关概念的辨析,包括导数存在性、驻点、拐点等。
解题核心思路:
- 极值存在的必要条件:若函数在某点可导且取得极值,则该点导数为0(即驻点),但不可导点也可能为极值点。
- 极值与拐点的关系:极值点是函数值局部最小(或最大)的点,而拐点是函数凹凸性改变的点,二者无必然联系。
- 关键概念区分:明确“极值存在”与“导数存在”“拐点”等概念的独立性。
破题关键点:
- 选项B:极值存在的前提是函数在该点有定义,因此$f(x_0)$必然存在。
- 选项C:极小值点不一定是拐点,需通过凹凸性变化判断。
- 选项A和D:需结合可导性分析,但题目未明确可导条件,需注意逻辑严谨性。
选项分析
选项A:$f'(x_0)=0$
- 必要条件:若函数在$x_0$处可导且取得极小值,则$f'(x_0)=0$成立。
- 例外情况:若函数在$x_0$处不可导,可能仍有极小值,此时$f'(x_0)$不存在。
- 结论:不一定成立,但题目未明确可导条件,因此不能直接判定错误。
选项B:$f(x_0)$不存在
- 极值定义:函数在$x_0$处有极小值,必须满足$f(x_0)$存在且为局部最小值。
- 结论:明显错误,直接排除。
选项C:点$x_0$是拐点
- 拐点本质:拐点需满足函数凹凸性在该点改变,而极小值点仅涉及函数值的局部最小性。
- 反例:$f(x)=x^2$在$x=0$处有极小值,但此处无拐点。
- 结论:不一定成立,因此错误。
选项D:点$x_0$是驻点
- 驻点定义:驻点要求$f'(x_0)=0$,但若函数在$x_0$处不可导,则$x_0$不是驻点。
- 结论:不一定成立,但题目未明确可导条件,需结合选项B和C的确定性。