当x→0+时,sqrt (x+sqrt {x)}是x_________阶的无穷小.正确答案:低
当x→0+时,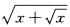 是x_________阶的无穷小.
是x_________阶的无穷小.
正确答案:低
题目解答
答案
解析: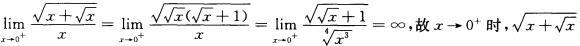 是x的低阶无穷小. 知识模块:函数、极限与连续
是x的低阶无穷小. 知识模块:函数、极限与连续
解析
考查要点:本题主要考查无穷小阶的比较方法,即通过极限判断两个无穷小量的阶数关系。
解题核心思路:
比较两个无穷小量的阶数,通常计算它们的比值的极限。若极限为0,则分子是分母的高阶无穷小;若极限为无穷大,则分子是分母的低阶无穷小;若极限为非零常数,则同阶。
破题关键点:
- 正确分解表达式:将$\sqrt{x+\sqrt{x}}$中的根号部分进行因式分解,提取出$x$的因子。
- 简化分式:将分式$\dfrac{\sqrt{x+\sqrt{x}}}{x}$转化为更易求极限的形式。
- 判断极限性质:通过分析简化后的表达式,确定极限是否为无穷大,从而得出阶数关系。
步骤1:分解根号内的表达式
将$\sqrt{x+\sqrt{x}}$中的根号部分分解:
$x + \sqrt{x} = \sqrt{x} \cdot (\sqrt{x} + 1)$
因此,原式可写为:
$\sqrt{x+\sqrt{x}} = \sqrt{\sqrt{x} \cdot (\sqrt{x} + 1)} = \sqrt{\sqrt{x}} \cdot \sqrt{\sqrt{x} + 1} = x^{1/4} \cdot \sqrt{\sqrt{x} + 1}$
步骤2:构造分式并简化
将分式$\dfrac{\sqrt{x+\sqrt{x}}}{x}$代入分解后的表达式:
$\frac{\sqrt{x+\sqrt{x}}}{x} = \frac{x^{1/4} \cdot \sqrt{\sqrt{x} + 1}}{x} = \frac{\sqrt{\sqrt{x} + 1}}{x^{3/4}}$
步骤3:求极限
当$x \to 0^+$时,$\sqrt{x} \to 0$,因此$\sqrt{\sqrt{x} + 1} \to \sqrt{0 + 1} = 1$,而分母$x^{3/4} \to 0$。此时分式趋近于$\dfrac{1}{0}$,即极限为无穷大:
$\lim_{x \to 0^+} \frac{\sqrt{\sqrt{x} + 1}}{x^{3/4}} = +\infty$
结论:
由于分式极限为无穷大,说明$\sqrt{x+\sqrt{x}}$是$x$的低阶无穷小。