题目
3.lim _(narrow infty )dfrac (1)({n)^2}[ ln dfrac (1)(n)+2ln dfrac (2)(n)+... +(n-1)ln dfrac (n-1)(n)] = ____
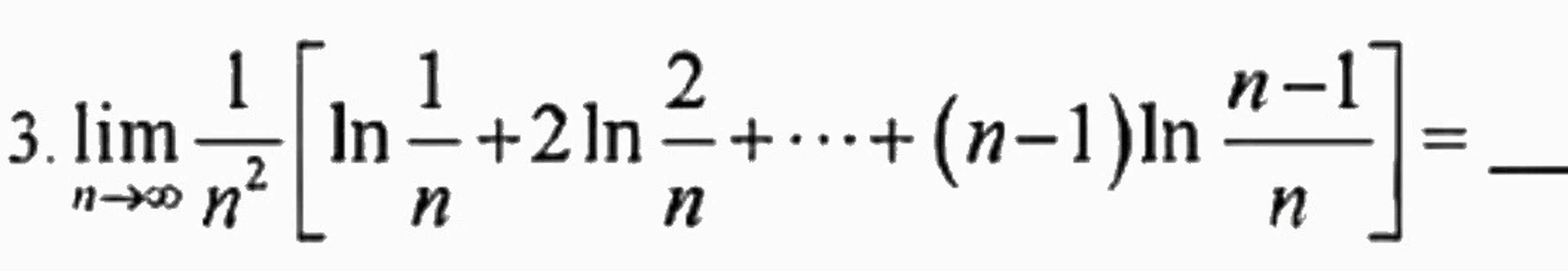
题目解答
答案
【】
步骤 1:将问题转化为求和形式
原问题可以写成求和形式:$\lim _{n\rightarrow \infty }\dfrac {1}{{n}^{2}}\sum_{k=1}^{n-1}k\ln \dfrac {k}{n}$
步骤 2:将求和形式转化为积分形式
由于求和项可以看作是函数$f(x) = x\ln x$在区间$[0,1]$上的黎曼和,因此可以将求和形式转化为积分形式:$\lim _{n\rightarrow \infty }\dfrac {1}{{n}^{2}}\sum_{k=1}^{n-1}k\ln \dfrac {k}{n} = \int_{0}^{1}x\ln x dx$
步骤 3:计算积分
计算积分$\int_{0}^{1}x\ln x dx$,使用分部积分法,设$u = \ln x$,$dv = x dx$,则$du = \frac{1}{x} dx$,$v = \frac{1}{2}x^2$,因此$\int_{0}^{1}x\ln x dx = \frac{1}{2}x^2\ln x|_{0}^{1} - \int_{0}^{1}\frac{1}{2}x dx = -\frac{1}{4}$
【答案】
$-\frac{1}{4}$
步骤 1:将问题转化为求和形式
原问题可以写成求和形式:$\lim _{n\rightarrow \infty }\dfrac {1}{{n}^{2}}\sum_{k=1}^{n-1}k\ln \dfrac {k}{n}$
步骤 2:将求和形式转化为积分形式
由于求和项可以看作是函数$f(x) = x\ln x$在区间$[0,1]$上的黎曼和,因此可以将求和形式转化为积分形式:$\lim _{n\rightarrow \infty }\dfrac {1}{{n}^{2}}\sum_{k=1}^{n-1}k\ln \dfrac {k}{n} = \int_{0}^{1}x\ln x dx$
步骤 3:计算积分
计算积分$\int_{0}^{1}x\ln x dx$,使用分部积分法,设$u = \ln x$,$dv = x dx$,则$du = \frac{1}{x} dx$,$v = \frac{1}{2}x^2$,因此$\int_{0}^{1}x\ln x dx = \frac{1}{2}x^2\ln x|_{0}^{1} - \int_{0}^{1}\frac{1}{2}x dx = -\frac{1}{4}$
【答案】
$-\frac{1}{4}$
解析
步骤 1:将问题转化为求和形式
原问题可以写成求和形式:$\lim _{n\rightarrow \infty }\dfrac {1}{{n}^{2}}\sum_{k=1}^{n-1}k\ln \dfrac {k}{n}$
步骤 2:将求和形式转化为积分形式
由于求和项可以看作是函数$f(x) = x\ln x$在区间$[0,1]$上的黎曼和,因此可以将求和形式转化为积分形式:$\lim _{n\rightarrow \infty }\dfrac {1}{{n}^{2}}\sum_{k=1}^{n-1}k\ln \dfrac {k}{n} = \int_{0}^{1}x\ln x dx$
步骤 3:计算积分
计算积分$\int_{0}^{1}x\ln x dx$,使用分部积分法,设$u = \ln x$,$dv = x dx$,则$du = \frac{1}{x} dx$,$v = \frac{1}{2}x^2$,因此$\int_{0}^{1}x\ln x dx = \frac{1}{2}x^2\ln x|_{0}^{1} - \int_{0}^{1}\frac{1}{2}x dx = -\frac{1}{4}$
原问题可以写成求和形式:$\lim _{n\rightarrow \infty }\dfrac {1}{{n}^{2}}\sum_{k=1}^{n-1}k\ln \dfrac {k}{n}$
步骤 2:将求和形式转化为积分形式
由于求和项可以看作是函数$f(x) = x\ln x$在区间$[0,1]$上的黎曼和,因此可以将求和形式转化为积分形式:$\lim _{n\rightarrow \infty }\dfrac {1}{{n}^{2}}\sum_{k=1}^{n-1}k\ln \dfrac {k}{n} = \int_{0}^{1}x\ln x dx$
步骤 3:计算积分
计算积分$\int_{0}^{1}x\ln x dx$,使用分部积分法,设$u = \ln x$,$dv = x dx$,则$du = \frac{1}{x} dx$,$v = \frac{1}{2}x^2$,因此$\int_{0}^{1}x\ln x dx = \frac{1}{2}x^2\ln x|_{0}^{1} - \int_{0}^{1}\frac{1}{2}x dx = -\frac{1}{4}$