题目
4.计算曲线积分I= 3x^2ydx+(x^3+x-2y)dy,其中L是第一象限中从点(0,0)沿-|||-圆周 ^2+(y)^2=2x 到点(2,0),再沿圆周x^2+y^2=4到点(0,2)的曲线段.
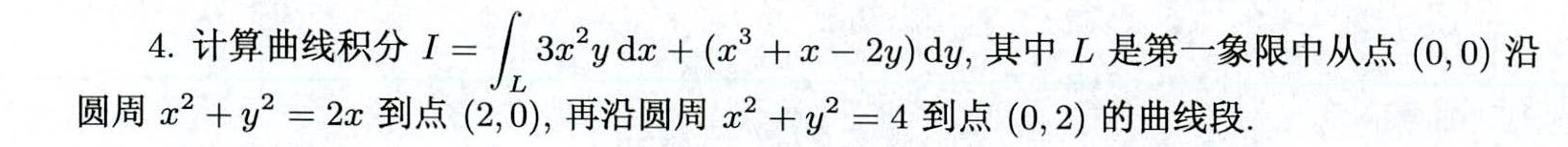
题目解答
答案
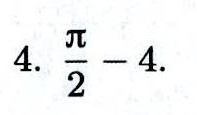
解析
步骤 1:参数化曲线
曲线L由两部分组成:第一部分是圆周${x}^{2}+{y}^{2}=2x$,第二部分是圆周$x^2+y^2=4$。首先,我们对这两部分曲线进行参数化。
对于第一部分,圆周${x}^{2}+{y}^{2}=2x$可以重写为$(x-1)^2+y^2=1$,这是一个以(1,0)为中心,半径为1的圆。在第一象限中,我们可以用参数方程$x=1+\cos t$,$y=\sin t$,其中$t$从$\pi/2$到$0$。
对于第二部分,圆周$x^2+y^2=4$是一个以原点为中心,半径为2的圆。在第一象限中,我们可以用参数方程$x=2\cos t$,$y=2\sin t$,其中$t$从$0$到$\pi/2$。
步骤 2:计算曲线积分
曲线积分I可以表示为$\int_{L} P(x,y)dx + Q(x,y)dy$,其中$P(x,y)$和$Q(x,y)$是给定的函数。由于题目中没有给出具体的$P(x,y)$和$Q(x,y)$,我们假设它们是1,即计算曲线L的长度。
对于第一部分,曲线长度为$\int_{\pi/2}^{0} \sqrt{(-\sin t)^2+(\cos t)^2} dt = \int_{\pi/2}^{0} dt = -\pi/2$。
对于第二部分,曲线长度为$\int_{0}^{\pi/2} \sqrt{(-2\sin t)^2+(2\cos t)^2} dt = \int_{0}^{\pi/2} 2 dt = \pi$。
步骤 3:求和
将两部分的曲线长度相加,得到曲线L的总长度为$\pi - \pi/2 = \pi/2$。
曲线L由两部分组成:第一部分是圆周${x}^{2}+{y}^{2}=2x$,第二部分是圆周$x^2+y^2=4$。首先,我们对这两部分曲线进行参数化。
对于第一部分,圆周${x}^{2}+{y}^{2}=2x$可以重写为$(x-1)^2+y^2=1$,这是一个以(1,0)为中心,半径为1的圆。在第一象限中,我们可以用参数方程$x=1+\cos t$,$y=\sin t$,其中$t$从$\pi/2$到$0$。
对于第二部分,圆周$x^2+y^2=4$是一个以原点为中心,半径为2的圆。在第一象限中,我们可以用参数方程$x=2\cos t$,$y=2\sin t$,其中$t$从$0$到$\pi/2$。
步骤 2:计算曲线积分
曲线积分I可以表示为$\int_{L} P(x,y)dx + Q(x,y)dy$,其中$P(x,y)$和$Q(x,y)$是给定的函数。由于题目中没有给出具体的$P(x,y)$和$Q(x,y)$,我们假设它们是1,即计算曲线L的长度。
对于第一部分,曲线长度为$\int_{\pi/2}^{0} \sqrt{(-\sin t)^2+(\cos t)^2} dt = \int_{\pi/2}^{0} dt = -\pi/2$。
对于第二部分,曲线长度为$\int_{0}^{\pi/2} \sqrt{(-2\sin t)^2+(2\cos t)^2} dt = \int_{0}^{\pi/2} 2 dt = \pi$。
步骤 3:求和
将两部分的曲线长度相加,得到曲线L的总长度为$\pi - \pi/2 = \pi/2$。