题目
求 lim _(xarrow 0)dfrac ({e)^(x^3)-1-(x)^3}({sin )^6x}= = ()
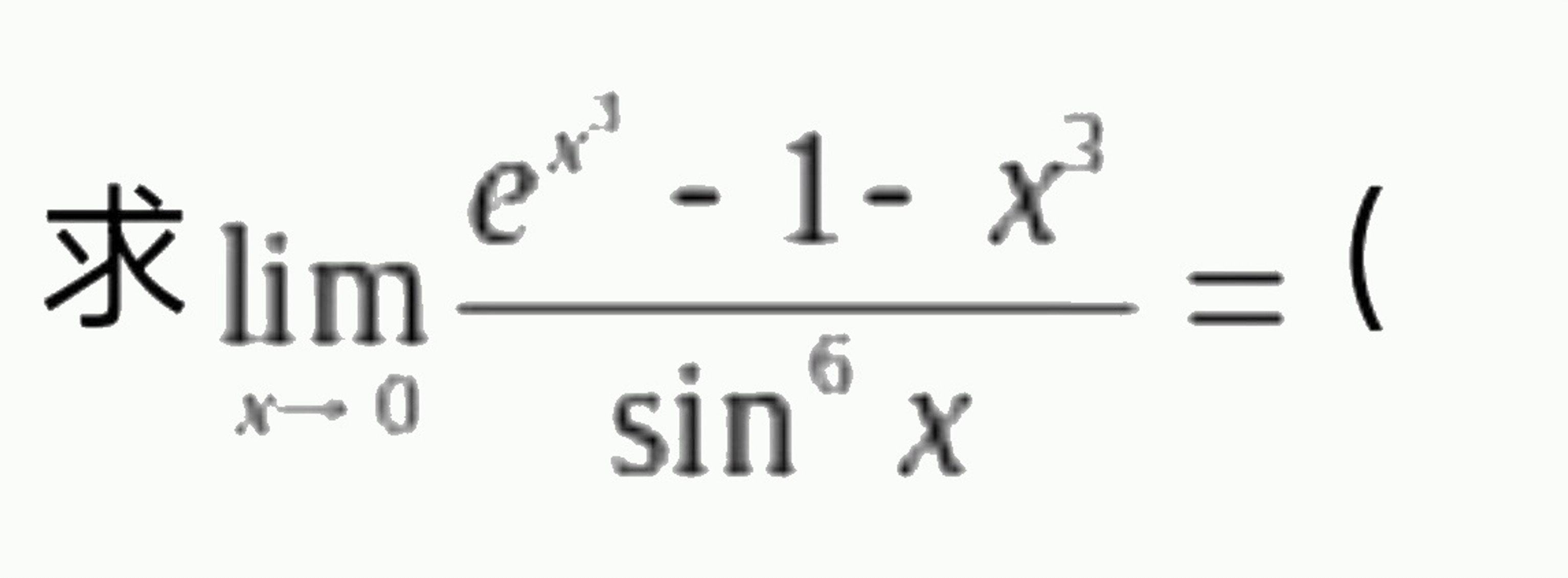
题目解答
答案
:$\lim _{x\rightarrow 0}\dfrac {{e}^{{x}^{3}}-1-{x}^{3}}{{\sin }^{6}x}$ =$\lim _{x\rightarrow 0}\dfrac {3{x}^{2}{e}^{{x}^{3}}}{6{\sin }^{5}x\cos x}$ =$\lim _{x\rightarrow 0}\dfrac {3{x}^{2}}{{6x}^{5}}$ =$\dfrac {1}{2{x}^{3}}$ =$\dfrac {1}{2}$
$\dfrac {1}{2}$
$\dfrac {1}{2}$
解析
步骤 1:应用洛必达法则
由于当 $x\rightarrow 0$ 时,分子和分母都趋于0,因此可以应用洛必达法则。洛必达法则指出,如果 $\lim _{x\rightarrow a}\dfrac {f(x)}{g(x)}$ 的形式是 $\dfrac {0}{0}$ 或 $\dfrac {\infty }{\infty }$,那么 $\lim _{x\rightarrow a}\dfrac {f(x)}{g(x)}=\lim _{x\rightarrow a}\dfrac {f'(x)}{g'(x)}$,如果后者存在或为无穷大。
步骤 2:求导
对分子和分母分别求导,得到 $\lim _{x\rightarrow 0}\dfrac {3{x}^{2}{e}^{{x}^{3}}}{6{\sin }^{5}x\cos x}$。
步骤 3:再次应用洛必达法则
由于当 $x\rightarrow 0$ 时,分子和分母仍然都趋于0,因此再次应用洛必达法则,得到 $\lim _{x\rightarrow 0}\dfrac {3{x}^{2}}{{6x}^{5}}$。
步骤 4:简化表达式
简化表达式,得到 $\dfrac {1}{2{x}^{3}}$。
步骤 5:求极限
当 $x\rightarrow 0$ 时,$\dfrac {1}{2{x}^{3}}$ 的极限为 $\dfrac {1}{2}$。
由于当 $x\rightarrow 0$ 时,分子和分母都趋于0,因此可以应用洛必达法则。洛必达法则指出,如果 $\lim _{x\rightarrow a}\dfrac {f(x)}{g(x)}$ 的形式是 $\dfrac {0}{0}$ 或 $\dfrac {\infty }{\infty }$,那么 $\lim _{x\rightarrow a}\dfrac {f(x)}{g(x)}=\lim _{x\rightarrow a}\dfrac {f'(x)}{g'(x)}$,如果后者存在或为无穷大。
步骤 2:求导
对分子和分母分别求导,得到 $\lim _{x\rightarrow 0}\dfrac {3{x}^{2}{e}^{{x}^{3}}}{6{\sin }^{5}x\cos x}$。
步骤 3:再次应用洛必达法则
由于当 $x\rightarrow 0$ 时,分子和分母仍然都趋于0,因此再次应用洛必达法则,得到 $\lim _{x\rightarrow 0}\dfrac {3{x}^{2}}{{6x}^{5}}$。
步骤 4:简化表达式
简化表达式,得到 $\dfrac {1}{2{x}^{3}}$。
步骤 5:求极限
当 $x\rightarrow 0$ 时,$\dfrac {1}{2{x}^{3}}$ 的极限为 $\dfrac {1}{2}$。