题目
求过一点 M(1,1,-1) 和直线 M(1,1,-1) 的平面方程.
求过一点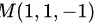 
和直线 
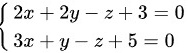的平面方程.
题目解答
答案
首先，我们求直线的方向向量。观察直线的参数方程，我们可以得到直线的方向向量为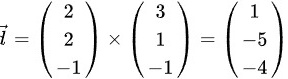
。接下来，我们可以使用点法式来求解平面方程。根据点法式，平面方程为
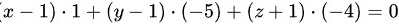，化简得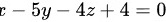
。所以，过点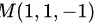
解析
步骤 1：求直线的方向向量
给定的直线由两个平面方程表示，我们可以通过求解这两个平面的法向量的叉积来得到直线的方向向量。平面 $2x+2y-z+3=0$ 的法向量为 $\overrightarrow{n_1}=(2,2,-1)$，平面 $3x+y-z+5=0$ 的法向量为 $\overrightarrow{n_2}=(3,1,-1)$。直线的方向向量 $\overrightarrow{l}$ 为 $\overrightarrow{n_1}$ 和 $\overrightarrow{n_2}$ 的叉积，即 $\overrightarrow{l}=\overrightarrow{n_1} \times \overrightarrow{n_2}$。
步骤 2：计算叉积
$\overrightarrow{l}=\overrightarrow{n_1} \times \overrightarrow{n_2} = \begin{vmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ 2 & 2 & -1 \\ 3 & 1 & -1 \end{vmatrix} = \overrightarrow{i}(2 \times (-1) - (-1) \times 1) - \overrightarrow{j}(2 \times (-1) - (-1) \times 3) + \overrightarrow{k}(2 \times 1 - 2 \times 3) = \overrightarrow{i}(-2 + 1) - \overrightarrow{j}(-2 + 3) + \overrightarrow{k}(2 - 6) = -\overrightarrow{i} - \overrightarrow{j} - 4\overrightarrow{k} = (-1, -1, -4)$。
步骤 3：求平面方程
已知平面过点 M(1,1,-1) 和直线的方向向量 $\overrightarrow{l}=(-1, -1, -4)$，我们可以使用点法式来求解平面方程。点法式为 $(x-x_0)\cdot a + (y-y_0)\cdot b + (z-z_0)\cdot c = 0$，其中 $(x_0, y_0, z_0)$ 是平面上的点，$(a, b, c)$ 是平面的法向量。由于直线的方向向量是平面的法向量，所以平面方程为 $(x-1)\cdot (-1) + (y-1)\cdot (-1) + (z+1)\cdot (-4) = 0$，化简得 $-x - y - 4z + 6 = 0$，即 $x + y + 4z - 6 = 0$。
给定的直线由两个平面方程表示，我们可以通过求解这两个平面的法向量的叉积来得到直线的方向向量。平面 $2x+2y-z+3=0$ 的法向量为 $\overrightarrow{n_1}=(2,2,-1)$，平面 $3x+y-z+5=0$ 的法向量为 $\overrightarrow{n_2}=(3,1,-1)$。直线的方向向量 $\overrightarrow{l}$ 为 $\overrightarrow{n_1}$ 和 $\overrightarrow{n_2}$ 的叉积，即 $\overrightarrow{l}=\overrightarrow{n_1} \times \overrightarrow{n_2}$。
步骤 2：计算叉积
$\overrightarrow{l}=\overrightarrow{n_1} \times \overrightarrow{n_2} = \begin{vmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ 2 & 2 & -1 \\ 3 & 1 & -1 \end{vmatrix} = \overrightarrow{i}(2 \times (-1) - (-1) \times 1) - \overrightarrow{j}(2 \times (-1) - (-1) \times 3) + \overrightarrow{k}(2 \times 1 - 2 \times 3) = \overrightarrow{i}(-2 + 1) - \overrightarrow{j}(-2 + 3) + \overrightarrow{k}(2 - 6) = -\overrightarrow{i} - \overrightarrow{j} - 4\overrightarrow{k} = (-1, -1, -4)$。
步骤 3：求平面方程
已知平面过点 M(1,1,-1) 和直线的方向向量 $\overrightarrow{l}=(-1, -1, -4)$，我们可以使用点法式来求解平面方程。点法式为 $(x-x_0)\cdot a + (y-y_0)\cdot b + (z-z_0)\cdot c = 0$，其中 $(x_0, y_0, z_0)$ 是平面上的点，$(a, b, c)$ 是平面的法向量。由于直线的方向向量是平面的法向量，所以平面方程为 $(x-1)\cdot (-1) + (y-1)\cdot (-1) + (z+1)\cdot (-4) = 0$，化简得 $-x - y - 4z + 6 = 0$，即 $x + y + 4z - 6 = 0$。