1.已知 = 1,2,3,4,5,6,7 , = 2,4,5 , = 1,3,5,7 , 求 cap ((C)_(C)cdot B), ((C)_(( ))A)cap ((C)_(1):B).-|||-2.设 = x|x 是平行四边形或梯形), = x|x 是平行四边形), = x|x 是菱形), = x|x 是矩-|||-形),求 B∩C, CsB,CsA.-|||-3.图中U是全集,A,B是U的两个子集,用阴影表示:-|||-(1) ((C)_((1.A))cap ((C)_(C)B:;-|||-(2) ((C)_(U)A)cup (C,B).-|||-U-|||-A B-|||-(1)-|||-U-|||-A B-|||-(2)-|||-(第3题)

考查要点：

1. 集合的基本运算，包括补集、交集、并集的定义与运算规则。
2. 集合关系的实际应用，如几何图形的分类与集合表示。
3. 维恩图的阴影表示，通过图形理解集合运算的结果。

解题核心思路：

• 补集运算：明确全集范围，补集是全集中不属于原集合的元素。
• 交集与并集：通过元素共性或特性判断集合关系。
• 几何集合关系：菱形、矩形、平行四边形、梯形的包含与交集关系。

第1题

求 $A \cap (C_U B)$ 和 $(C_U A) \cap (C_U B)$

步骤1：求补集

• $C_U B = U - B = \{2,4,6\}$
• $C_U A = U - A = \{1,3,6,7\}$

步骤2：求交集

• $A \cap (C_U B) = \{2,4,5\} \cap \{2,4,6\} = \{2,4\}$
• $(C_U A) \cap (C_U B) = \{1,3,6,7\} \cap \{2,4,6\} = \{6\}$

第2题

求 $B \cap C$，$C_S B$，$C_S A$

步骤1：分析集合关系

• 菱形（B）与矩形（C）的交集：既是菱形又是矩形的图形是正方形。
• $C_S B$：属于$S$但不属于$B$的图形，即平行四边形（非菱形）或梯形。
• $C_S A$：属于$S$但不属于$A$的图形，即梯形。

步骤2：结论

• $B \cap C = \{\text{x | x是正方形}\}$
• $C_S B = \{\text{x | x是平行四边形或梯形，且不是菱形}\}$
• $C_S A = \{\text{x | x是梯形}\}$

第3题

用阴影表示集合运算

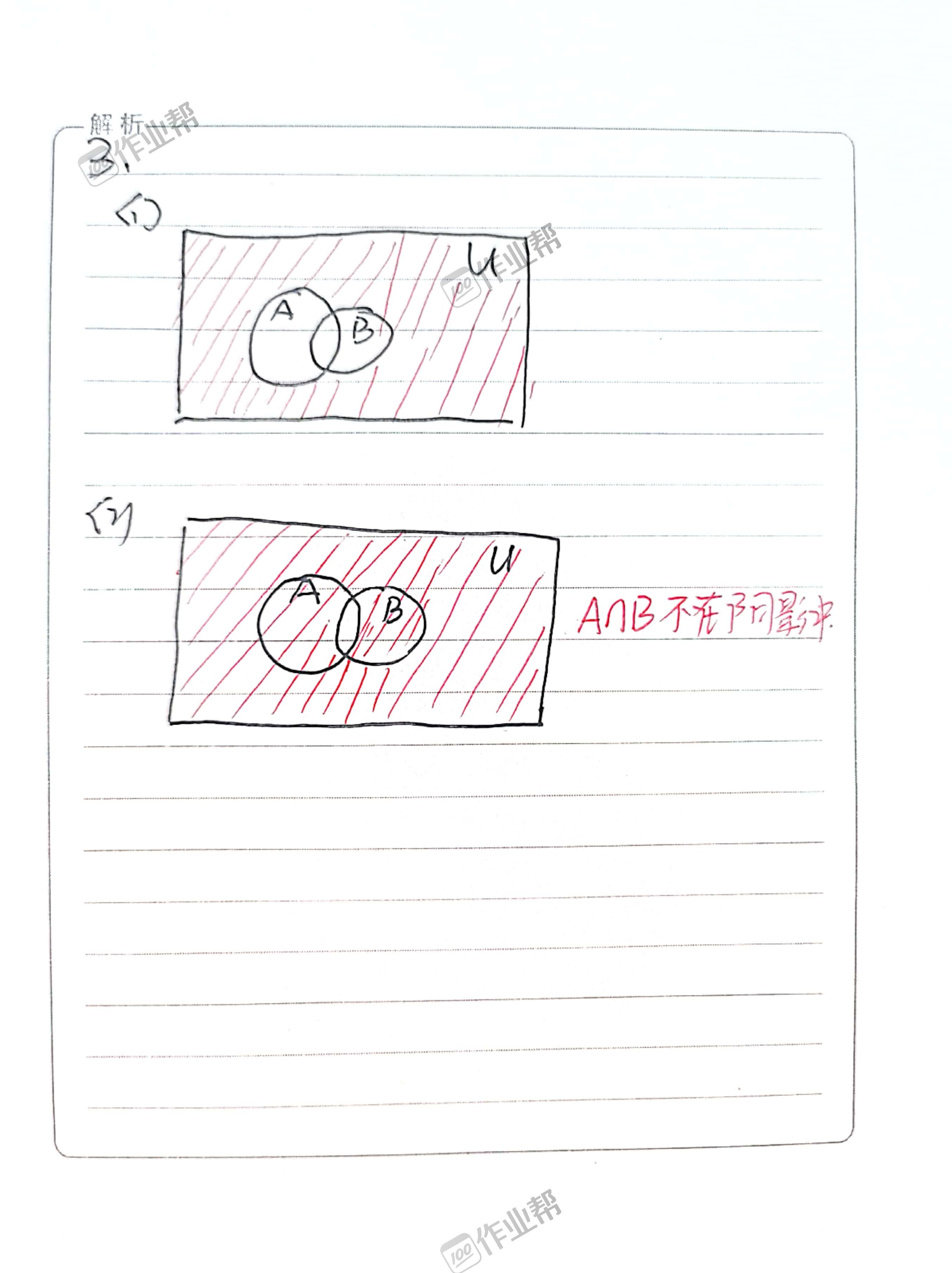
(1) $(C_U A) \cap (C_U B)$

• 含义：既不属于$A$也不属于$B$的元素。
• 阴影区域：全集$U$中，$A$和$B$的交集外的区域（德摩根定律：$C_U (A \cup B)$）。

(2) $(C_U A) \cup (C_U B)$

• 含义：不属于$A$或不属于$B$的元素。
• 阴影区域：全集$U$中，$A$和$B$的交集外的区域（德摩根定律：$C_U (A \cap B)$）。