求微分方程 '=yln dfrac (y)(x) 的通解.
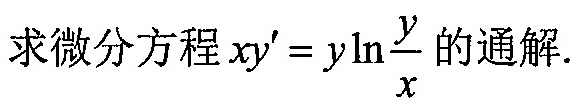
题目解答
答案

解析
考查要点:本题主要考查齐次微分方程的解法,通过变量代换将方程转化为可分离变量方程,进而求解通解。
解题核心思路:
- 识别齐次方程:方程右边为$\ln \dfrac{y}{x}$,属于齐次函数形式。
- 变量代换:令$y = ux$,将方程转化为关于$u$和$x$的可分离变量方程。
- 分离变量与积分:通过分离变量法积分求解,注意积分常数的处理。
- 回代与整理:将中间变量$u$替换回原变量$y$,并整理得到通解。
破题关键点:
- 正确代换:通过$y = ux$简化方程结构。
- 分离变量技巧:将方程变形为$\dfrac{1}{u(\ln u -1)} du = \dfrac{1}{x} dx$。
- 积分与化简:通过积分并整理对数表达式,最终得到通解形式。
步骤1:变量代换
令$y = ux$,则$y' = u + x u'$。代入原方程$xy' = y \ln \dfrac{y}{x}$,得:
$x(u + x u') = ux \cdot \ln u$
化简后:
$u + x u' = u \ln u \quad \Rightarrow \quad x u' = u (\ln u - 1)$
步骤2:分离变量
将方程改写为:
$\frac{du}{dx} = \frac{u (\ln u - 1)}{x}$
分离变量:
$\frac{1}{u (\ln u - 1)} du = \frac{1}{x} dx$
步骤3:积分求解
对两边积分:
$\int \frac{1}{u (\ln u - 1)} du = \int \frac{1}{x} dx$
令$t = \ln u - 1$,则$dt = \dfrac{1}{u} du$,左边积分变为:
$\int \frac{1}{t} dt = \ln |t| + C_1 = \ln |\ln u - 1| + C_1$
右边积分结果为:
$\ln |x| + C_2$
合并常数,得:
$\ln |\ln u - 1| = \ln |x| + C$
步骤4:回代与整理
指数化简:
$|\ln u - 1| = C |x| \quad \Rightarrow \quad \ln u - 1 = C x$
解得:
$\ln u = 1 + C x \quad \Rightarrow \quad u = e^{1 + C x}$
回代$u = \dfrac{y}{x}$,得通解:
$y = x e^{1 + C x}$
步骤5:验证特殊情况
当$u (\ln u - 1) = 0$时:
- 若$u = 0$,则$y = 0$,代入原方程成立。
- 若$\ln u - 1 = 0$,则$u = e$,对应$y = e x$,代入原方程也成立。
此时$C = 0$时,通解$y = x e^{1 + 0 \cdot x} = e x$,故无需额外添加解。