题目
19.求函数=√(x^2+y^2+z^2)在约束条件=√(x^2+y^2+z^2)与=√(x^2+y^2+z^2)=√(x^2+y^2+z^2)下的最值.
19.求函数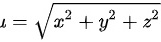 在约束条件
在约束条件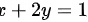 与
与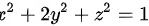
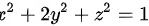 下的最值.
下的最值.
题目解答
答案
解:构造拉格朗日函数为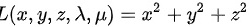
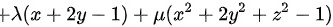 ,然后分别对
,然后分别对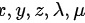 分别求偏导数,并令其为零,可得如下方程组:
分别求偏导数,并令其为零,可得如下方程组: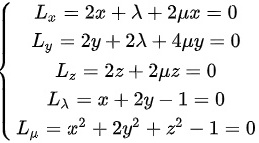 ,
,
解该方程组可得两组解为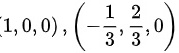 ,代入函数
,代入函数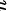 可得最大值为
可得最大值为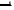 ,最小值为
,最小值为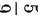 .
.
解析
步骤 1:构造拉格朗日函数
构造拉格朗日函数为$I(x,y,z,\lambda ,\mu )={x}^{2}+{y}^{2}+{z}^{2}+\lambda (x+2y-1)+\mu ({x}^{2}+2{y}^{2}+{z}^{2}-1)$,其中$\lambda$和$\mu$是拉格朗日乘子。
步骤 2:求偏导数
分别对$x,y,z,\lambda ,\mu$求偏导数,并令其为零,得到方程组:
\[
\begin{cases}
\frac{\partial I}{\partial x} = 2x + \lambda + 2\mu x = 0 \\
\frac{\partial I}{\partial y} = 2y + 2\lambda + 4\mu y = 0 \\
\frac{\partial I}{\partial z} = 2z + 2\mu z = 0 \\
\frac{\partial I}{\partial \lambda} = x + 2y - 1 = 0 \\
\frac{\partial I}{\partial \mu} = {x}^{2} + 2{y}^{2} + {z}^{2} - 1 = 0
\end{cases}
\]
步骤 3:解方程组
解上述方程组可得两组解为$(1,0,0)$和$(-\dfrac {1}{3},\dfrac {2}{3},0)$。
步骤 4:代入函数求最值
将上述两组解代入函数$t=\sqrt {{x}^{2}+{y}^{2}+{z}^{2}}$中,可得最大值为1,最小值为$\dfrac{1}{3}$。
构造拉格朗日函数为$I(x,y,z,\lambda ,\mu )={x}^{2}+{y}^{2}+{z}^{2}+\lambda (x+2y-1)+\mu ({x}^{2}+2{y}^{2}+{z}^{2}-1)$,其中$\lambda$和$\mu$是拉格朗日乘子。
步骤 2:求偏导数
分别对$x,y,z,\lambda ,\mu$求偏导数,并令其为零,得到方程组:
\[
\begin{cases}
\frac{\partial I}{\partial x} = 2x + \lambda + 2\mu x = 0 \\
\frac{\partial I}{\partial y} = 2y + 2\lambda + 4\mu y = 0 \\
\frac{\partial I}{\partial z} = 2z + 2\mu z = 0 \\
\frac{\partial I}{\partial \lambda} = x + 2y - 1 = 0 \\
\frac{\partial I}{\partial \mu} = {x}^{2} + 2{y}^{2} + {z}^{2} - 1 = 0
\end{cases}
\]
步骤 3:解方程组
解上述方程组可得两组解为$(1,0,0)$和$(-\dfrac {1}{3},\dfrac {2}{3},0)$。
步骤 4:代入函数求最值
将上述两组解代入函数$t=\sqrt {{x}^{2}+{y}^{2}+{z}^{2}}$中,可得最大值为1,最小值为$\dfrac{1}{3}$。