题目
设S=(0,1,2,3),⑧为模4乘法,即"⑧x,y∈S, x⑧y=(xy)mod 4问〈S,⑧〉是否构成群?为什么?
设S={0,1,2,3}, 为模4乘法,即
为模4乘法,即
"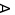 x,y∈S, x
x,y∈S, x y=(xy)mod 4
y=(xy)mod 4
问〈S, 〉是否构成群?为什么?
〉是否构成群?为什么?
题目解答
答案
解:(1) 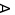 x,y∈S, x
x,y∈S, x y=(xy)mod 4
y=(xy)mod 4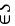 ,
, 是S上的代数运算。
是S上的代数运算。
(2) 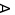 x,y,z∈S,设xy=4k+r
x,y,z∈S,设xy=4k+r 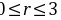
(x y)
y) z =((xy)mod 4)
z =((xy)mod 4) z=r
z=r z=(rz)mod 4
z=(rz)mod 4
=(4kz+rz)mod 4=((4k+r)z)mod 4 =(xyz)mod 4
同理x (y
(y z) =(xyz)mod 4
z) =(xyz)mod 4
所以,(x y)
y) z = x
z = x (y
(y z),结合律成立。
z),结合律成立。
(3) 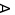 x∈S, (x
x∈S, (x 1)=(1
1)=(1 x)=x,,所以1是单位元。
x)=x,,所以1是单位元。
(4)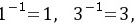 0和2没有逆元
0和2没有逆元
所以,〈S, 〉不构成群
〉不构成群
解析
步骤 1:验证代数运算
首先,我们需要验证⑧是否是S上的代数运算。即对于任意的x,y∈S,x⑧y=(xy)mod 4是否仍然属于S。
步骤 2:验证结合律
接下来,我们需要验证结合律是否成立。即对于任意的x,y,z∈S,(x⑧y)⑧z是否等于x⑧(y⑧z)。
步骤 3:验证单位元
然后,我们需要验证是否存在单位元。即是否存在一个元素e∈S,使得对于任意的x∈S,x⑧e=e⑧x=x。
步骤 4:验证逆元
最后,我们需要验证每个元素是否都有逆元。即对于任意的x∈S,是否存在一个元素y∈S,使得x⑧y=y⑧x=e,其中e是单位元。
首先,我们需要验证⑧是否是S上的代数运算。即对于任意的x,y∈S,x⑧y=(xy)mod 4是否仍然属于S。
步骤 2:验证结合律
接下来,我们需要验证结合律是否成立。即对于任意的x,y,z∈S,(x⑧y)⑧z是否等于x⑧(y⑧z)。
步骤 3:验证单位元
然后,我们需要验证是否存在单位元。即是否存在一个元素e∈S,使得对于任意的x∈S,x⑧e=e⑧x=x。
步骤 4:验证逆元
最后,我们需要验证每个元素是否都有逆元。即对于任意的x∈S,是否存在一个元素y∈S,使得x⑧y=y⑧x=e,其中e是单位元。