题目
已知sin 0.32=0.314567 sin 0.34=0.333487 sin 0.36=0.352274,用抛物线插值计算sin 0.32=0.314567 sin 0.34=0.333487 sin 0.36=0.352274的值并估计截断误差。(拉格朗日二次插值)
已知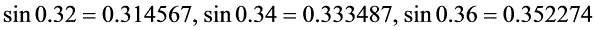 ,用抛物线插值计算
,用抛物线插值计算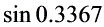 的值并估计截断误差。(拉格朗日二次插值)
的值并估计截断误差。(拉格朗日二次插值)
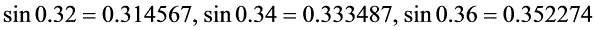 ,用抛物线插值计算
,用抛物线插值计算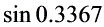 的值并估计截断误差。(拉格朗日二次插值)
的值并估计截断误差。(拉格朗日二次插值)题目解答
答案
解:由插值条件,其抛物线插值函数为
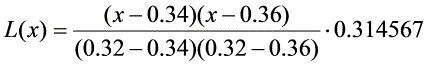
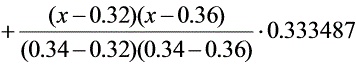
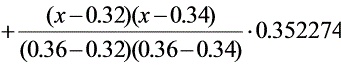
将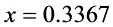 代入,计算可得:
代入,计算可得: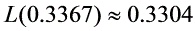 。
。
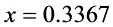 代入,计算可得:
代入,计算可得: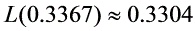 。
。其余项为: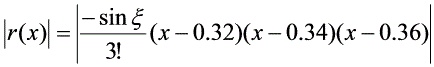 其中,
其中,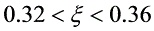
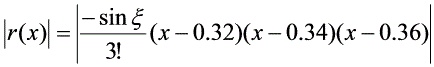 其中,
其中,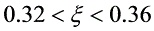
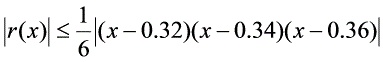
故误差的上界为:
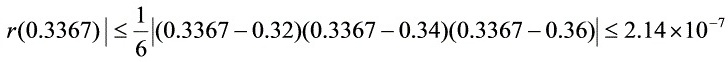 。
。解析
步骤 1:构造拉格朗日插值多项式
根据题目给出的三个点$(0.32, 0.314567)$, $(0.34, 0.333487)$, $(0.36, 0.352274)$,构造拉格朗日插值多项式$L(x)$。拉格朗日插值多项式的一般形式为:
$$
L(x) = \sum_{i=0}^{n} y_i \prod_{\substack{j=0 \\ j \neq i}}^{n} \frac{x - x_j}{x_i - x_j}
$$
其中,$n=2$,$x_i$和$y_i$分别是插值点的横坐标和纵坐标。将给定的点代入,得到:
$$
L(x) = \frac{(x-0.34)(x-0.36)}{(0.32-0.34)(0.32-0.36)} \cdot 0.314567 + \frac{(x-0.32)(x-0.36)}{(0.34-0.32)(0.34-0.36)} \cdot 0.333487 + \frac{(x-0.32)(x-0.34)}{(0.36-0.32)(0.36-0.34)} \cdot 0.352274
$$
步骤 2:计算$L(0.3367)$
将$x=0.3367$代入$L(x)$,计算$L(0.3367)$的值。
步骤 3:估计截断误差
拉格朗日插值的截断误差公式为:
$$
R(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!} \prod_{i=0}^{n} (x - x_i)
$$
其中,$n=2$,$f^{(n+1)}(\xi)$是插值函数的$(n+1)$阶导数在区间$[0.32, 0.36]$内的某个点$\xi$处的值。对于$\sin x$,其三阶导数为$-\sin x$,因此:
$$
|R(x)| \leq \frac{1}{3!} \cdot |(x-0.32)(x-0.34)(x-0.36)|
$$
将$x=0.3367$代入,计算截断误差的上界。
【答案】
【解析】
步骤 1:构造拉格朗日插值多项式
$$
L(x) = \frac{(x-0.34)(x-0.36)}{(0.32-0.34)(0.32-0.36)} \cdot 0.314567 + \frac{(x-0.32)(x-0.36)}{(0.34-0.32)(0.34-0.36)} \cdot 0.333487 + \frac{(x-0.32)(x-0.34)}{(0.36-0.32)(0.36-0.34)} \cdot 0.352274
$$
步骤 2:计算$L(0.3367)$
$$
L(0.3367) \approx 0.3304
$$
步骤 3:估计截断误差
$$
|R(x)| \leq \frac{1}{6} \cdot |(0.3367-0.32)(0.3367-0.34)(0.3367-0.36)|
$$
根据题目给出的三个点$(0.32, 0.314567)$, $(0.34, 0.333487)$, $(0.36, 0.352274)$,构造拉格朗日插值多项式$L(x)$。拉格朗日插值多项式的一般形式为:
$$
L(x) = \sum_{i=0}^{n} y_i \prod_{\substack{j=0 \\ j \neq i}}^{n} \frac{x - x_j}{x_i - x_j}
$$
其中,$n=2$,$x_i$和$y_i$分别是插值点的横坐标和纵坐标。将给定的点代入,得到:
$$
L(x) = \frac{(x-0.34)(x-0.36)}{(0.32-0.34)(0.32-0.36)} \cdot 0.314567 + \frac{(x-0.32)(x-0.36)}{(0.34-0.32)(0.34-0.36)} \cdot 0.333487 + \frac{(x-0.32)(x-0.34)}{(0.36-0.32)(0.36-0.34)} \cdot 0.352274
$$
步骤 2:计算$L(0.3367)$
将$x=0.3367$代入$L(x)$,计算$L(0.3367)$的值。
步骤 3:估计截断误差
拉格朗日插值的截断误差公式为:
$$
R(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!} \prod_{i=0}^{n} (x - x_i)
$$
其中,$n=2$,$f^{(n+1)}(\xi)$是插值函数的$(n+1)$阶导数在区间$[0.32, 0.36]$内的某个点$\xi$处的值。对于$\sin x$,其三阶导数为$-\sin x$,因此:
$$
|R(x)| \leq \frac{1}{3!} \cdot |(x-0.32)(x-0.34)(x-0.36)|
$$
将$x=0.3367$代入,计算截断误差的上界。
【答案】
【解析】
步骤 1:构造拉格朗日插值多项式
$$
L(x) = \frac{(x-0.34)(x-0.36)}{(0.32-0.34)(0.32-0.36)} \cdot 0.314567 + \frac{(x-0.32)(x-0.36)}{(0.34-0.32)(0.34-0.36)} \cdot 0.333487 + \frac{(x-0.32)(x-0.34)}{(0.36-0.32)(0.36-0.34)} \cdot 0.352274
$$
步骤 2:计算$L(0.3367)$
$$
L(0.3367) \approx 0.3304
$$
步骤 3:估计截断误差
$$
|R(x)| \leq \frac{1}{6} \cdot |(0.3367-0.32)(0.3367-0.34)(0.3367-0.36)|
$$