lim _(xarrow 0)((dfrac {1+{2)^x}(2))}^dfrac (1{x)}= __
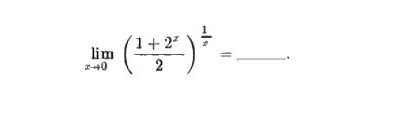
题目解答
答案

解析
考查要点:本题主要考查指数函数的极限计算,涉及自然对数转换、泰勒展开或等价无穷小替换的应用,以及极限运算的技巧。
解题核心思路:
将原式转化为指数形式,利用自然对数简化计算。通过展开或替换,将复杂表达式转化为基本极限形式,最终结合指数函数还原结果。
破题关键点:
- 自然对数转换:将原式写成$e^{\lim f(x)}$的形式,简化指数部分的极限计算。
- 等价无穷小替换:当$x \to 0$时,$2^x -1 \sim x \ln 2$,用于简化对数内的表达式。
- 极限运算:通过代入等价无穷小或洛必达法则,求出指数部分的极限值。
步骤1:自然对数转换
原式可改写为:
$\lim_{x \to 0} \left( \frac{1 + 2^x}{2} \right)^{\frac{1}{x}} = \exp\left( \lim_{x \to 0} \frac{1}{x} \ln \left( \frac{1 + 2^x}{2} \right) \right)$
步骤2:简化对数表达式
当$x \to 0$时,$2^x \approx 1 + x \ln 2$(泰勒展开一阶项),代入得:
$\frac{1 + 2^x}{2} \approx \frac{1 + (1 + x \ln 2)}{2} = 1 + \frac{x \ln 2}{2}$
步骤3:应用等价无穷小
对数部分展开为:
$\ln\left(1 + \frac{x \ln 2}{2}\right) \approx \frac{x \ln 2}{2} \quad (\text{当} \ x \to 0)$
步骤4:计算指数部分的极限
将上述近似代入原式:
$\lim_{x \to 0} \frac{1}{x} \cdot \frac{x \ln 2}{2} = \frac{\ln 2}{2}$
步骤5:还原指数形式
最终结果为:
$\exp\left( \frac{\ln 2}{2} \right) = e^{\ln \sqrt{2}} = \sqrt{2}$