题目
求指导本题解题过程,谢谢您!六、(10分) =iint int (x+y+z)dxdydz, 其中Ω是由 =0, y=0 z=0 及-|||-x+y+z=1 所围成的立体域.
求指导本题解题过程,谢谢您!
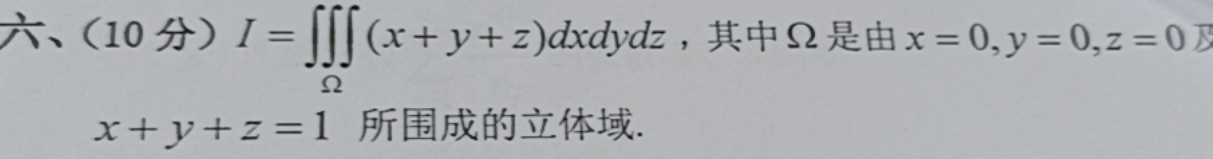
题目解答
答案

解析
步骤 1:确定积分区域
积分区域Ω是由平面x=0, y=0, z=0和x+y+z=1所围成的立体域。这是一个在第一卦限内的四面体,其顶点为(0,0,0), (1,0,0), (0,1,0), (0,0,1)。
步骤 2:设置积分
根据积分区域Ω,我们可以设置三重积分的积分限。由于Ω是四面体,我们可以选择z作为最外层的积分变量,y作为中间层,x作为最内层。因此,积分可以写为:
\[ I = \iiint_{\Omega} (x+y+z) \, dx \, dy \, dz \]
步骤 3:计算积分
首先,确定积分限。对于z,其范围是从0到1-x-y;对于y,其范围是从0到1-x;对于x,其范围是从0到1。因此,积分可以写为:
\[ I = \int_{0}^{1} \int_{0}^{1-x} \int_{0}^{1-x-y} (x+y+z) \, dz \, dy \, dx \]
步骤 4:计算内层积分
首先计算最内层的积分,即对z的积分:
\[ \int_{0}^{1-x-y} (x+y+z) \, dz = \left[ (x+y)z + \frac{1}{2}z^2 \right]_{0}^{1-x-y} = (x+y)(1-x-y) + \frac{1}{2}(1-x-y)^2 \]
\[ = (x+y)(1-x-y) + \frac{1}{2}(1-x-y)^2 = (x+y)(1-x-y) + \frac{1}{2}(1-2x-2y+x^2+2xy+y^2) \]
\[ = (x+y)(1-x-y) + \frac{1}{2}(1-2x-2y+x^2+2xy+y^2) \]
\[ = x+y-x^2-xy-y^2 + \frac{1}{2}(1-2x-2y+x^2+2xy+y^2) \]
\[ = x+y-x^2-xy-y^2 + \frac{1}{2} - x - y + \frac{1}{2}x^2 + xy + \frac{1}{2}y^2 \]
\[ = \frac{1}{2} - \frac{1}{2}x^2 - \frac{1}{2}y^2 \]
步骤 5:计算中间层积分
接下来计算对y的积分:
\[ \int_{0}^{1-x} \left( \frac{1}{2} - \frac{1}{2}x^2 - \frac{1}{2}y^2 \right) \, dy = \left[ \frac{1}{2}y - \frac{1}{2}x^2y - \frac{1}{6}y^3 \right]_{0}^{1-x} \]
\[ = \frac{1}{2}(1-x) - \frac{1}{2}x^2(1-x) - \frac{1}{6}(1-x)^3 \]
\[ = \frac{1}{2}(1-x) - \frac{1}{2}x^2(1-x) - \frac{1}{6}(1-3x+3x^2-x^3) \]
\[ = \frac{1}{2}(1-x) - \frac{1}{2}x^2(1-x) - \frac{1}{6} + \frac{1}{2}x - \frac{1}{2}x^2 + \frac{1}{6}x^3 \]
\[ = \frac{1}{2} - \frac{1}{2}x - \frac{1}{2}x^2 + \frac{1}{2}x^3 - \frac{1}{6} + \frac{1}{2}x - \frac{1}{2}x^2 + \frac{1}{6}x^3 \]
\[ = \frac{1}{3} - \frac{2}{3}x^2 + \frac{2}{3}x^3 \]
步骤 6:计算最外层积分
最后计算对x的积分:
\[ \int_{0}^{1} \left( \frac{1}{3} - \frac{2}{3}x^2 + \frac{2}{3}x^3 \right) \, dx = \left[ \frac{1}{3}x - \frac{2}{9}x^3 + \frac{1}{6}x^4 \right]_{0}^{1} \]
\[ = \frac{1}{3} - \frac{2}{9} + \frac{1}{6} = \frac{6}{18} - \frac{4}{18} + \frac{3}{18} = \frac{5}{18} \]
积分区域Ω是由平面x=0, y=0, z=0和x+y+z=1所围成的立体域。这是一个在第一卦限内的四面体,其顶点为(0,0,0), (1,0,0), (0,1,0), (0,0,1)。
步骤 2:设置积分
根据积分区域Ω,我们可以设置三重积分的积分限。由于Ω是四面体,我们可以选择z作为最外层的积分变量,y作为中间层,x作为最内层。因此,积分可以写为:
\[ I = \iiint_{\Omega} (x+y+z) \, dx \, dy \, dz \]
步骤 3:计算积分
首先,确定积分限。对于z,其范围是从0到1-x-y;对于y,其范围是从0到1-x;对于x,其范围是从0到1。因此,积分可以写为:
\[ I = \int_{0}^{1} \int_{0}^{1-x} \int_{0}^{1-x-y} (x+y+z) \, dz \, dy \, dx \]
步骤 4:计算内层积分
首先计算最内层的积分,即对z的积分:
\[ \int_{0}^{1-x-y} (x+y+z) \, dz = \left[ (x+y)z + \frac{1}{2}z^2 \right]_{0}^{1-x-y} = (x+y)(1-x-y) + \frac{1}{2}(1-x-y)^2 \]
\[ = (x+y)(1-x-y) + \frac{1}{2}(1-x-y)^2 = (x+y)(1-x-y) + \frac{1}{2}(1-2x-2y+x^2+2xy+y^2) \]
\[ = (x+y)(1-x-y) + \frac{1}{2}(1-2x-2y+x^2+2xy+y^2) \]
\[ = x+y-x^2-xy-y^2 + \frac{1}{2}(1-2x-2y+x^2+2xy+y^2) \]
\[ = x+y-x^2-xy-y^2 + \frac{1}{2} - x - y + \frac{1}{2}x^2 + xy + \frac{1}{2}y^2 \]
\[ = \frac{1}{2} - \frac{1}{2}x^2 - \frac{1}{2}y^2 \]
步骤 5:计算中间层积分
接下来计算对y的积分:
\[ \int_{0}^{1-x} \left( \frac{1}{2} - \frac{1}{2}x^2 - \frac{1}{2}y^2 \right) \, dy = \left[ \frac{1}{2}y - \frac{1}{2}x^2y - \frac{1}{6}y^3 \right]_{0}^{1-x} \]
\[ = \frac{1}{2}(1-x) - \frac{1}{2}x^2(1-x) - \frac{1}{6}(1-x)^3 \]
\[ = \frac{1}{2}(1-x) - \frac{1}{2}x^2(1-x) - \frac{1}{6}(1-3x+3x^2-x^3) \]
\[ = \frac{1}{2}(1-x) - \frac{1}{2}x^2(1-x) - \frac{1}{6} + \frac{1}{2}x - \frac{1}{2}x^2 + \frac{1}{6}x^3 \]
\[ = \frac{1}{2} - \frac{1}{2}x - \frac{1}{2}x^2 + \frac{1}{2}x^3 - \frac{1}{6} + \frac{1}{2}x - \frac{1}{2}x^2 + \frac{1}{6}x^3 \]
\[ = \frac{1}{3} - \frac{2}{3}x^2 + \frac{2}{3}x^3 \]
步骤 6:计算最外层积分
最后计算对x的积分:
\[ \int_{0}^{1} \left( \frac{1}{3} - \frac{2}{3}x^2 + \frac{2}{3}x^3 \right) \, dx = \left[ \frac{1}{3}x - \frac{2}{9}x^3 + \frac{1}{6}x^4 \right]_{0}^{1} \]
\[ = \frac{1}{3} - \frac{2}{9} + \frac{1}{6} = \frac{6}{18} - \frac{4}{18} + \frac{3}{18} = \frac{5}{18} \]