题目
试确定常数A,B,C的值,使得 ^x(1+Bx+C(x)^2)=1+Ax+o((x)^3), 其中o(x^3)是当x-|||-→0 时比x^3高阶的无穷小.
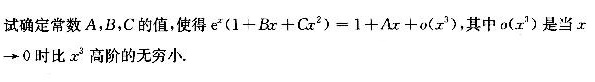
题目解答
答案

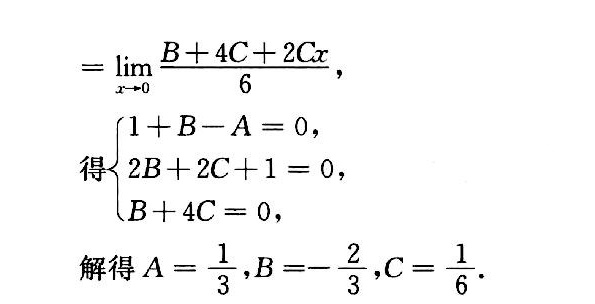
解析
步骤 1:确定等式两边的泰勒展开
首先,我们需要对等式两边进行泰勒展开。等式左边是 ${e}^{x}(1-Bx+C{x}^{2})$,等式右边是 $1+Ax+o({x}^{3})$。我们需要将左边的表达式展开到$x^3$的项,以便与右边的表达式进行比较。
步骤 2:计算 ${e}^{x}$ 的泰勒展开
${e}^{x}$ 的泰勒展开为 ${e}^{x} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + o(x^3)$。
步骤 3:将 ${e}^{x}$ 的泰勒展开代入原式
将 ${e}^{x}$ 的泰勒展开代入原式,得到:
${e}^{x}(1-Bx+C{x}^{2}) = (1 + x + \frac{x^2}{2} + \frac{x^3}{6} + o(x^3))(1-Bx+C{x}^{2})$。
步骤 4:展开并整理
将上式展开并整理,得到:
$1 + x + \frac{x^2}{2} + \frac{x^3}{6} - Bx - Bx^2 - \frac{Bx^3}{2} + Cx^2 + Cx^3 + o(x^3)$
$= 1 + (1-B)x + (\frac{1}{2} - B + C)x^2 + (\frac{1}{6} - \frac{B}{2} + C)x^3 + o(x^3)$。
步骤 5:比较系数
将上式与 $1+Ax+o({x}^{3})$ 比较系数,得到:
$1-B = A$,
$\frac{1}{2} - B + C = 0$,
$\frac{1}{6} - \frac{B}{2} + C = 0$。
步骤 6:解方程组
解方程组 $\left \{ \begin{matrix} 1-B=A,\\ \frac{1}{2} - B + C = 0,\\ \frac{1}{6} - \frac{B}{2} + C = 0,\end{matrix} \right.$ 得到 $A=1$,$B=0$,$C=-\frac{1}{2}$。
首先,我们需要对等式两边进行泰勒展开。等式左边是 ${e}^{x}(1-Bx+C{x}^{2})$,等式右边是 $1+Ax+o({x}^{3})$。我们需要将左边的表达式展开到$x^3$的项,以便与右边的表达式进行比较。
步骤 2:计算 ${e}^{x}$ 的泰勒展开
${e}^{x}$ 的泰勒展开为 ${e}^{x} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + o(x^3)$。
步骤 3:将 ${e}^{x}$ 的泰勒展开代入原式
将 ${e}^{x}$ 的泰勒展开代入原式,得到:
${e}^{x}(1-Bx+C{x}^{2}) = (1 + x + \frac{x^2}{2} + \frac{x^3}{6} + o(x^3))(1-Bx+C{x}^{2})$。
步骤 4:展开并整理
将上式展开并整理,得到:
$1 + x + \frac{x^2}{2} + \frac{x^3}{6} - Bx - Bx^2 - \frac{Bx^3}{2} + Cx^2 + Cx^3 + o(x^3)$
$= 1 + (1-B)x + (\frac{1}{2} - B + C)x^2 + (\frac{1}{6} - \frac{B}{2} + C)x^3 + o(x^3)$。
步骤 5:比较系数
将上式与 $1+Ax+o({x}^{3})$ 比较系数,得到:
$1-B = A$,
$\frac{1}{2} - B + C = 0$,
$\frac{1}{6} - \frac{B}{2} + C = 0$。
步骤 6:解方程组
解方程组 $\left \{ \begin{matrix} 1-B=A,\\ \frac{1}{2} - B + C = 0,\\ \frac{1}{6} - \frac{B}{2} + C = 0,\end{matrix} \right.$ 得到 $A=1$,$B=0$,$C=-\frac{1}{2}$。