题目
椭圆 dfrac ({x)^2}(m)+dfrac ({y)^2}(8)=1 的焦距是2,则m的值是 ()-|||-A.9 B.7或10-|||-C.7或9 D.25

题目解答
答案
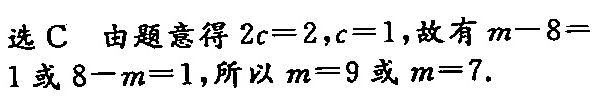
解析
考查要点:本题主要考查椭圆的标准方程及焦距的计算,需根据分母大小判断椭圆的长轴方向,进而应用焦距公式求解参数。
解题核心思路:
- 确定椭圆的长轴方向:比较分母$m$和$8$的大小,判断椭圆的长轴是在$x$轴还是$y$轴。
- 应用焦距公式:根据长轴方向,选择对应的焦距公式$c^2 = a^2 - b^2$,结合已知焦距$2c=2$,建立方程求解$m$。
破题关键点:
- 分情况讨论:需分$m > 8$和$m < 8$两种情况,分别对应长轴在$x$轴和$y$轴。
- 正确代入公式:注意$a$和$b$的取值随长轴方向变化,避免混淆。
步骤1:确定焦距$c$的值
已知焦距$2c = 2$,解得$c = 1$。
步骤2:分情况讨论椭圆的长轴方向
-
情况1:当$m > 8$时
椭圆的长轴在$x$轴上,此时$a^2 = m$,$b^2 = 8$。
根据焦距公式$c^2 = a^2 - b^2$,代入$c=1$得:
$1^2 = m - 8 \implies m = 9.$ -
情况2:当$m < 8$时
椭圆的长轴在$y$轴上,此时$a^2 = 8$,$b^2 = m$。
根据焦距公式$c^2 = a^2 - b^2$,代入$c=1$得:
$1^2 = 8 - m \implies m = 7.$
结论:$m$的值为$9$或$7$,对应选项C。