题目
求级数sum _(n=1)^infty dfrac ({4)^n}(2+{n)^3}(x)^n的收敛区间?
求级数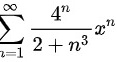 的收敛区间?
的收敛区间?
题目解答
答案
解:
因为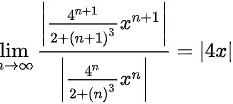
根据比值判别法,
当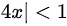 ,
,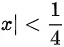 绝对收敛
绝对收敛
当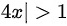 ,
,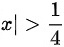 绝对收敛
绝对收敛
当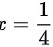 时,
时,
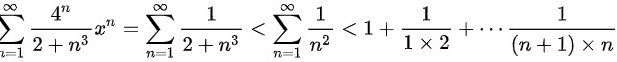
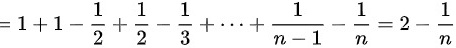
所以当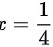 时,原级数收敛。
时,原级数收敛。
当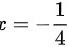 时,级数是
时,级数是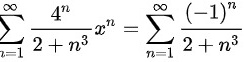
而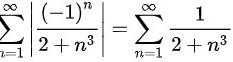 收敛,
收敛,
所以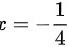 时,原级数收敛。
时,原级数收敛。
综上所述,原级数的收敛域是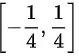
解析
步骤 1:应用比值判别法
首先,我们应用比值判别法来确定级数的收敛半径。比值判别法的公式为:
$$
\lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| = L
$$
其中,$a_n = \frac{4^n}{2+n^3}x^n$。我们需要计算:
$$
\lim_{n \to \infty} \left| \frac{\frac{4^{n+1}}{2+(n+1)^3}x^{n+1}}{\frac{4^n}{2+n^3}x^n} \right|
$$
步骤 2:简化表达式
简化上述表达式,我们得到:
$$
\lim_{n \to \infty} \left| \frac{4^{n+1}x^{n+1}(2+n^3)}{4^n x^n (2+(n+1)^3)} \right| = \lim_{n \to \infty} \left| \frac{4x(2+n^3)}{2+(n+1)^3} \right|
$$
步骤 3:计算极限
计算上述极限,我们得到:
$$
\lim_{n \to \infty} \left| \frac{4x(2+n^3)}{2+(n+1)^3} \right| = \lim_{n \to \infty} \left| \frac{4x}{1+\frac{3n^2+3n+1}{n^3}} \right| = 4|x|
$$
步骤 4:确定收敛半径
根据比值判别法,当$4|x| < 1$时,级数绝对收敛。因此,收敛半径为$\frac{1}{4}$。
步骤 5:检查端点
当$x = \frac{1}{4}$时,级数变为$\sum _{n=1}^{\infty }\dfrac {1}{2+{n}^{3}}$,这是一个收敛的级数。
当$x = -\frac{1}{4}$时,级数变为$\sum _{n=1}^{\infty }\dfrac {{(-1)}^{n}}{2+{n}^{3}}$,这是一个收敛的交错级数。
首先,我们应用比值判别法来确定级数的收敛半径。比值判别法的公式为:
$$
\lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| = L
$$
其中,$a_n = \frac{4^n}{2+n^3}x^n$。我们需要计算:
$$
\lim_{n \to \infty} \left| \frac{\frac{4^{n+1}}{2+(n+1)^3}x^{n+1}}{\frac{4^n}{2+n^3}x^n} \right|
$$
步骤 2:简化表达式
简化上述表达式,我们得到:
$$
\lim_{n \to \infty} \left| \frac{4^{n+1}x^{n+1}(2+n^3)}{4^n x^n (2+(n+1)^3)} \right| = \lim_{n \to \infty} \left| \frac{4x(2+n^3)}{2+(n+1)^3} \right|
$$
步骤 3:计算极限
计算上述极限,我们得到:
$$
\lim_{n \to \infty} \left| \frac{4x(2+n^3)}{2+(n+1)^3} \right| = \lim_{n \to \infty} \left| \frac{4x}{1+\frac{3n^2+3n+1}{n^3}} \right| = 4|x|
$$
步骤 4:确定收敛半径
根据比值判别法,当$4|x| < 1$时,级数绝对收敛。因此,收敛半径为$\frac{1}{4}$。
步骤 5:检查端点
当$x = \frac{1}{4}$时,级数变为$\sum _{n=1}^{\infty }\dfrac {1}{2+{n}^{3}}$,这是一个收敛的级数。
当$x = -\frac{1}{4}$时,级数变为$\sum _{n=1}^{\infty }\dfrac {{(-1)}^{n}}{2+{n}^{3}}$,这是一个收敛的交错级数。