题目
初值问题 =sqrt {{x)^2-(x)^2(y)^2+1-(y)^2} y(0)=-dfrac (1)(2) .
初值问题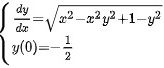 的解为( )
的解为( )
A 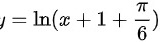
B 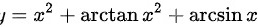
C 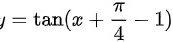
D 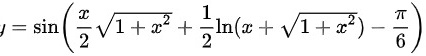
题目解答
答案
针对本题,有两个条件,分别为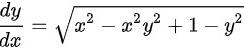
和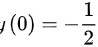 ,ABCD四个选项必须同时满足以上两个条件才可。
,ABCD四个选项必须同时满足以上两个条件才可。
首先判断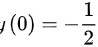
所以分析ABCD四个选项,
如果ABCD满足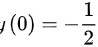 ,则符合条件。
,则符合条件。
如果ABCD满足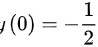 ,则不是正确的答案。
,则不是正确的答案。
对于A选项: 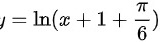
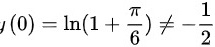
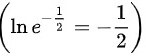
∴不是正确的答案。
对于B选项: 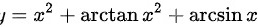
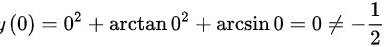
∴不是正确的答案。
对于C选项: 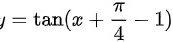
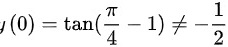
∴不是正确的答案。
对于D选项: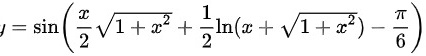
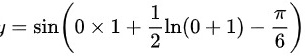
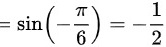
∴符合条件。
所以只有选项D符合条件。
综上,使用简单的排除法得到答案为D。
解析
步骤 1:验证初值条件
首先,我们需要验证每个选项在$x=0$时的值是否等于$-\dfrac{1}{2}$,因为这是初值条件。
步骤 2:计算每个选项在$x=0$时的值
对于A选项:$y=\ln (x+1+\dfrac{\pi}{6})$
$y(0)=\ln (1+\dfrac{\pi}{6})\neq -\dfrac{1}{2}$
对于B选项:$y={x}^{2}+\arctan {x}^{2}+\arctan x$
$y(0)={0}^{2}+\arctan {0}^{2}+\arctan 0=0\neq -\dfrac{1}{2}$
对于C选项:$y=\tan (x+\dfrac{\pi}{4}-1)$
$y(0)=\tan (\dfrac{\pi}{4}-1)\neq -\dfrac{1}{2}$
对于D选项:$y=\sin (\dfrac{x}{2}\sqrt{1+{x}^{2}}+\dfrac{1}{2}\ln (x+\sqrt{1+{x}^{2}})-\dfrac{\pi}{6})$
$y(0)=\sin (0\times 1+\dfrac{1}{2}\ln (0+1)-\dfrac{\pi}{6})$
$=\sin (-\dfrac{\pi}{6})=-\dfrac{1}{2}$
步骤 3:验证微分方程
由于只有D选项满足初值条件,我们只需验证D选项是否满足微分方程。
$y=\sin (\dfrac{x}{2}\sqrt{1+{x}^{2}}+\dfrac{1}{2}\ln (x+\sqrt{1+{x}^{2}})-\dfrac{\pi}{6})$
计算$\dfrac{dy}{dx}$,并验证是否等于$\sqrt{{x}^{2}-{x}^{2}{y}^{2}+1-{y}^{2}}$。
首先,我们需要验证每个选项在$x=0$时的值是否等于$-\dfrac{1}{2}$,因为这是初值条件。
步骤 2:计算每个选项在$x=0$时的值
对于A选项:$y=\ln (x+1+\dfrac{\pi}{6})$
$y(0)=\ln (1+\dfrac{\pi}{6})\neq -\dfrac{1}{2}$
对于B选项:$y={x}^{2}+\arctan {x}^{2}+\arctan x$
$y(0)={0}^{2}+\arctan {0}^{2}+\arctan 0=0\neq -\dfrac{1}{2}$
对于C选项:$y=\tan (x+\dfrac{\pi}{4}-1)$
$y(0)=\tan (\dfrac{\pi}{4}-1)\neq -\dfrac{1}{2}$
对于D选项:$y=\sin (\dfrac{x}{2}\sqrt{1+{x}^{2}}+\dfrac{1}{2}\ln (x+\sqrt{1+{x}^{2}})-\dfrac{\pi}{6})$
$y(0)=\sin (0\times 1+\dfrac{1}{2}\ln (0+1)-\dfrac{\pi}{6})$
$=\sin (-\dfrac{\pi}{6})=-\dfrac{1}{2}$
步骤 3:验证微分方程
由于只有D选项满足初值条件,我们只需验证D选项是否满足微分方程。
$y=\sin (\dfrac{x}{2}\sqrt{1+{x}^{2}}+\dfrac{1}{2}\ln (x+\sqrt{1+{x}^{2}})-\dfrac{\pi}{6})$
计算$\dfrac{dy}{dx}$,并验证是否等于$\sqrt{{x}^{2}-{x}^{2}{y}^{2}+1-{y}^{2}}$。