题目
若3 0 0-|||-A= 0 a b-|||-0 2 3与3 0 0-|||-A= 0 a b-|||-0 2 3相似，则（ ）.(A)a=0,b=-1;(B)a=0,b=1;(C)a=1,b=0;(D)a=-1,b=0;
若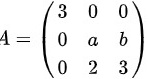
与
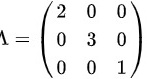相似，则（ ）.
(A)a=0,b=-1;
(B)a=0,b=1;
(C)a=1,b=0;
(D)a=-1,b=0;
题目解答
答案
答案为：A
∵
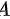与
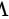相似
∴
；
∵
∴
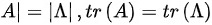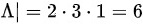
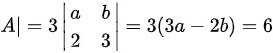
∴3a-2b=2
根据矩阵的迹相等，有：3+3+a=2+3+1=6
∴a=0
∴b=-1
所以选A
解析
步骤 1：计算矩阵的行列式
根据相似矩阵的性质，两个相似矩阵的行列式相等。计算矩阵的行列式，得到：
$$
|A| = 2 \cdot 3 \cdot 1 = 6
$$
步骤 2：计算矩阵的迹
根据相似矩阵的性质，两个相似矩阵的迹相等。计算矩阵的迹，得到：
$$
tr(A) = 3 + 3 + a = 2 + 3 + 1 = 6
$$
步骤 3：求解a和b
根据矩阵的迹相等，有：
$$
3 + 3 + a = 6
$$
解得：
$$
a = 0
$$
根据矩阵的行列式相等，有：
$$
3a - 2b = 2
$$
将a=0代入上式，解得：
$$
b = -1
$$
根据相似矩阵的性质，两个相似矩阵的行列式相等。计算矩阵的行列式，得到：
$$
|A| = 2 \cdot 3 \cdot 1 = 6
$$
步骤 2：计算矩阵的迹
根据相似矩阵的性质，两个相似矩阵的迹相等。计算矩阵的迹，得到：
$$
tr(A) = 3 + 3 + a = 2 + 3 + 1 = 6
$$
步骤 3：求解a和b
根据矩阵的迹相等，有：
$$
3 + 3 + a = 6
$$
解得：
$$
a = 0
$$
根据矩阵的行列式相等，有：
$$
3a - 2b = 2
$$
将a=0代入上式，解得：
$$
b = -1
$$